Ιδιοδιανύσματα και ιδιοτιμές πίνακα
Έστω ένας τελεστής Α, ο οποίος δρα πάνω σε ένα διάνυσμα |x>. Το αποτέλεσμα θα είναι ένα νέο διάνυσμα |y>, σύμφωνα με τον ορισμό του τελεστή, εν γένει διαφορετικό από το |x>, δηλ.
Α|x>=|y>.
Για κάθε τελεστή Α, υπάρχουν παρόλα αυτά κάποια χαρακτηριστικά διανύσματα, τέτοια ώστε η δράση του Α πάνω σε αυτά απλώς τα πολλαπλασιάζει με έναν αριθμό, λ, δηλαδή
Α|x>=λ|x>
Τα διανύσματα αυτά λέγονται ιδιοδιανύσματα του τελεστή Α και οι αριθμοί λ λέγονται ιδιοτιμές του Α και είναι χαρακτηριστικά μεγέθη του τελεστή Α.
Ανακαλώντας τώρα τη συζήτηση προηγούμενου κεφαλαίου σύμφωνα με την οποία ένας τελεστής σε δεδομένη βάση μπορεί να αναπαρασταθεί από έναν πίνακα, τα πιο πάνω μπορούν να μεταφερθούν αυτούσια και στη δράση πινάκων, στους οποίους θα εστιαστούμε στη συνέχεια. Ξεκινάμε με τον ορισμό ιδιοδιανυσμάτων και ιδιοτιμών.
Έστω ένας τετραγωνικός πίνακας (α), ο οποίος δρα πάνω σε ένα διάνυσμα (πίνακα στήλη) |x>. Το αποτέλεσμα θα είναι ένα νέο διάνυσμα (πίνακας στήλη) |y>, δηλαδή
(α)|x>=|y>.
Για κάθε πίνακα (α), σε αναλογία με τον αντίστοιχο τελεστή, έστω Α, υπάρχουν κάποια χαρακτηριστικά διανύσματα, τέτοια ώστε η δράση του (α) πάνω σε αυτά αφήνει αναλλοίωτη τη διεύθυνσή τους, και απλώς τα πολλαπλασιάζει με έναν αριθμό (δηλαδή αλλάζει μόνο το μέτρο τους˙ τα «διαστέλλει» ή τα «συστέλλει», χωρίς να τους αλλάζει τη διεύθυνση), δηλαδή
(α)|x>=λ|x> (1)
Τα διανύσματα αυτά, |x>, για τα οποία ισχύει η (1) λέγονται ιδιοδιανύσματα του πίνακα (α), και οι αριθμοί λ, οι οποίοι στην ουσία ισοδυναμούν με τον (α) όσον αφορά τη δράση πάνω στα ιδιοδιανύσματα, λέγονται ιδιοτιμές του (α) και είναι χαρακτηριστικοί αριθμοί του (α). (Μπορούμε να πούμε ότι ο (α) πάνω στα ιδιοδιανύσματα εκφυλίζεται στον αριθμό λ ή ότι ο λ πάνω στο ιδιοδιάνυσμα αντικαθιστά τη δράση του (α).)
Για κάθε ιδιοδιάνυσμα υπάρχει μία ιδιοτιμή, που ικανοποιεί την (1). Πρσέξτε ότι τα ιδιοδιανύσματα όπως ορίζονται στην (1) ορίζονται με απροσδιοριστία μιας πολλαπλασιαστικής σταθεράς. Δηλαδή αν το |x> είναι ιδιοδιάνυσμα με ιδιοτιμή λ, τότε και το κ|χ> (κ αριθμός) είναι επίσης ιδιοδιάνυσμα, με την ίδια ιδιοτιμή. Θα μπορούσαμε να πούμε δηλαδή ότι η σχέση ορισμού των ιδιοδιανυσμάτων, Εξ. (1), ορίζει μόνο τη διεύθυνση των ιδιοδιανυσμάτων και όχι το μέτρο τους.
Τα ιδιοδιανύσματα και οι ιδιοτιμές παίζουν κεντρικό ρόλο σε προβλήματα Φυσικής, και Επιστήμης Υλικών. Εκεί οι ιδιοτιμές μπορούν να εκφράζουν, π.χ., τις επιτρεπτές τιμές ενέργειας ή ορμής ή στροφορμής των ηλεκτρονίων σε ένα άτομο, τις συχνότητες ταλάντωσης ενός συστήματος συζευγμένων ταλαντωτών (π.χ. ταλαντούμενων ατόμων) κοκ.
Η εύρεση των ιδιοδιανυσμάτων και των ιδιοτιμών ενός πίνακα λέγεται πρόβλημα ιδιοτιμής ή ιδιοτιμών.
Υπολογισμός ιδιοδιανυσμάτων και ιδιοτιμών
Έστω το πρόβλημα ιδιοτιμής
(α)|x>=λ|x>, (2)
όπου ο (α) είναι γνωστός τετραγωνικός πίνακας n×n, και ζητούνται οι αριθμοί λ και τα διανύσματα |x> (μη μηδενικά). Το παραπάνω σύστημα μπορεί να πάρει τη μορφή (α)|x>=λ(ε)|x> ή [(α)-λ(ε)]|x>=0, όπου (ε) είναι ο μοναδιαίος n×n πίνακας.
Παρατηρήστε ότι το σύστημα [(α)-λ(ε)]|x>=0 είναι ένα ομογενές n×n σύστημα. Σύμφωνα με την θεωρία επίλυσης ομογενών γραμμικών συστημάτων, η οποία αναφέρθηκε σε προηγούμενο κεφάλαιο, ένα τέτοιο σύστημα έχει μη μηδενικές λύσεις |x>, όπως είναι το ζητούμενό μας, αν και μόνο αν η ορίζουσα του πίνακά του, δηλαδή του (α)-λ(ε), είναι ίση με μηδέν. (Αν η ορίζουσα είναι διαφορετική από μηδέν τότε το σύστημα έχει μοναδική λύση, η οποία είναι η μηδενική).
Δηλαδή, το σύστημα (2) έχει μη μηδενικές λύσεις αν και μόνο αν
det[(α)-λ(ε)]=0 (3)
Η εξίσωση (3), η οποία είναι ένα πολυώνυμο ως προς λ, φ(λ), χρησιμοποιείται για τον υπολογισμό των ιδιοτιμών, λ, του πίνακα (α).
Παρατηρήστε ότι όταν ο (α) είναι n×n το φ(λ)=det[(α)-λ(ε)] είναι πολυώνυμο n βαθμού ως προς λ και άρα η εξίσωση det[(α)-λ(ε)]=0 έχει n ρίζες, δηλαδή n αριθμούς λ που την ικανοποιούν, δηλαδή ο πίνακας n×n έχει n ιδιοτιμές. Το πολυώνυμο φ(λ)=det[(α)-λ(ε)] λέγεται χαρακτηριστικό πολυώνυμο του πίνακα (α).
Για τον υπολογισμό του ιδιοδιανύσματος που αντιστοιχεί στην κάθε ιδιοτιμή θέτουμε στην εξίσωση (2) την συγκεκριμένη ιδιοτιμή και λύνουμε το ομογενές σύστημα που προκύπτει.
Όπως αναφέρθηκε και νωρίτερα, τα ιδιοδιανύσματα ορίζονται με απροσδιοριστία μιας πολλαπλασιαστικής σταθεράς, δηλαδή η εξίσωση (2) ορίζει μόνο τη διεύθυνση τους και όχι το μέτρο τους, το οποίο παραμένει αυθαίρετο. Τις περισσότερες φορές, στις εφαρμογές, ενδιαφερόμαστε για τα κανονικοποιημένα ιδιοδιανύσματα, δηλαδή τα ιδιοδιανύσματα που έχουν μέτρο μονάδα Στην περίπτωση αυτή υπολογίζουμε κατάλληλα την τιμή της πολλαπλασιαστικής σταθεράς ώστε το διάνυσμα που προκύπτει να έχει μέτρο μονάδα.
Εφαρμογές
(1) Υπολογίστε τις ιδιοτιμές και τα (κανονικοποιημένα) ιδιοδιανύσματα του πίνακα
![]()
Απάντηση: λ1=3, ![]() ή
ή ![]() , λ2=-3,
, λ2=-3, ![]() ή
ή ![]()
(2) Υπολογίστε τα ιδιοδιανύσματα και τις ιδιοτιμές του διαγώνιου πίνακα
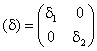
(3) Υπολογίστε τα ιδιοδιανύσματα και τις ιδιοτιμές του πίνακα
![]()
Το σύνολο των ιδιοτιμών ενός πίνακα λέγεται φάσμα του πίνακα.
Το πόσες φορές εμφανίζεται μια ιδιοτιμή στο φάσμα ενός πίνακα λέγεται αλγεβρική πολλαπλότητα της ιδιοτιμής.
Για τις ιδιοτιμές και τα ιδιοδιανύσματα πίνακα ισχύουν τα εξής:
(i) Το άθροισμα των ιδιοτιμών ενός πίνακα (α) ισούται με το ίχνος του (α).
(ii) Το γινόμενο των ιδιοτιμών ενός πίνακα (α) ισούται με την ορίζουσα του (α).
(iii) Για έναν οποιοδήποτε πίνακα (α) τα ιδιοδιανύσματά του που αντιστοιχούν σε διαφορετικές ιδιοτιμές είναι γραμμικά ανεξάρτητα.
Ελέγξτε τα παραπάνω, (i)-(iii), για τον πίνακα της Εφαρμογής (1).
Υπολογίστε τις ιδιοτιμές του αντιστρόφου ενός πίνακα, συναρτήσει των ιδιοτιμών του πίνακα. Αν ένας πίνακας (α) έχει κάποια ιδιοτιμή μηδέν, έχει ο (α) αντίστροφο?
Μια ιδιαίτερη και ενδιαφέρουσα κατηγορία πινάκων, όσον αφορά τα ιδιοδιανύσματα και τις ιδιοτιμές, είναι οι κανονικοί πίνακες. Υπενθυμίζουμε ότι ένας πίνακας (α) είναι κανονικός αν ισχύει η μεταθετική ιδιότητα στον πολλαπλασιασμό με τον συζυγή του, δηλαδή (α)(α)+=(α)+(α)
Αν (α) κανονικός πίνακας n×n τότε,
- Έχει πάντα n γραμμικά ανεξάρτητα ιδιοδιανύσματα.
- Τα ιδιοδιανύσματα που αντιστοιχούν σε διαφορετικές ιδιοτιμές είναι ορθογώνια.
- Τα ιδιοδιανύσματα του αποτελούν πλήρες σύστημα, και, δεδομένου ότι είναι γραμμικά ανεξάρτητα, αποτελούν βάση του διανυσματικού χώρου στον οποίο ορίζεται ο πίνακας.
Ειδικές περιπτώσεις κανονικών πινάκων είναι οι ερμιτιανοί ή αυτοπροσαρτημένοι πίνακες, οι αντιερμιτιανοί πίνακες και οι μοναδιακοί πίνακες.
- Οι ερμιτιανοί πίνακες, για τους οποίους (α)+=(α), οι οποίοι συναντώνται πολύ συχνά σε εφαρμογές της Φυσικής, έχουν πάντα πραγματικές ιδιοτιμές.
- Οι αντιερμιτιανοί πίνακες ((α)+=-(α)) έχουν φανταστικές ιδιοτιμές.
- Οι μοναδιακοί πίνακες ((α)+=(α)-1) έχουν ιδιοτιμές με μέτρο μονάδα.
Έστω 2×2 πίνακας (α) με ιδιοτιμές λ1 και λ2 και ιδιοδιανύσματα (γραμμικά ανεξάρτητα)
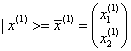 και
και
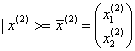 , και έστω ο πίνακας των
ιδιοδιανυσμάτων
, και έστω ο πίνακας των
ιδιοδιανυσμάτων
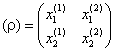 .
.
Τότε ισχύει ότι,
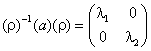 . (3)
. (3)
Δηλαδή το γινόμενο (ρ)-1(α)(ρ) δίνει έναν διαγώνιο πίνακα με στοιχεία τις ιδιοτιμές του (α), ή, όπως συχνά λέγεται, ο πίνακας (ρ) των ιδιοδιανυσμάτων διαγωνιοποιεί τον (α) με μετασχηματισμό ομοιότητας[1]. Ο υπολογισμός του γινομένου (ρ)-1(α)(ρ) λέγεται διαγωνιοποίση του πίνακα (α). Για αυτόν το λόγο, η εύρεση των ιδιοτιμών ενός πίνακα (α) λέγεται και διαγωνιοποίηση του (α).
Αντιστρέφοντας την (3), μπορούμε να πούμε ότι κάθε τετραγωνικός πίνακας (α) μπορεί να γραφεί στη μορφή (α)=(ρ)(λ)(ρ)-1, όπου (ρ) είναι ο πίνακας των ιδιοδιανυσμάτων του (α) και (λ) ο διαγώνιος πίνακας με στοιχεία τις ιδιοτιμές του (α).
Η διαγωνιοποίηση ενός πίνακα (α) είναι πάντα εφικτή όταν ο πίνακας (ρ) είναι αντιστρέψιμος, ή, ισοδύναμα, όταν τα ιδιοδιανύσματα του πίνακα (α) είναι γραμμικά ανεξάρτητα (αυτό, όπως μπορεί να εξαχθεί από τα παραπάνω, είναι πάντα εφικτό όταν ο πίνακας έχει διαφορετικές ιδιοτιμές. Στην περίπτωση επαναλαμβανόμενων ιδιοτιμών είναι εφικτό όταν ο πίνακας είναι κανονικός). Γενικά, μπορούμε να πούμε ότι η διαγωνιοποίηση πίνακα αποτυγχάνει μόνο σε περίπτωση επαναλαμβανόμενων ιδιοτιμών.
.
Εφαρμογή: Υπολογίστε τις ιδιοτιμές και τα ιδιοδιανύσματα των πινάκων
![]() και
και ![]() .
.
Μπορεί ο (α1) να διαγωνιοποιηθεί με μετασχηματισμό ομοιότητας; Πού οφείλεται η διαφορά των (α1) και (α2) όσον αφορά τα ιδιοδιανύσματα;