| (1) | |||
| (2) |
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ
Θα ξεκινήσουμε την παρουσίαση των γραμμικών συστημάτων με ένα
απλό παράδειγμα από τη Γεωμετρία, το οποίο θα μας βοηθήσει στην
κατανόηση των συστημάτων αυτών και των συνθηκών επιλυσιμότητάς τους.
Θεωρήστε τις ευθείες
| (1) | |||
| (2) |
Οι (1) και (2) αποτελούν ένα γραμμικό σύστημα εξισώσεων (γιατί
λέγεται γραμμικό;) το οποίο μπορεί να γραφεί, ισοδύναμα,
χρησιμοποιώντας άλγεβρα
πινάκων, ως
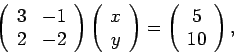 |
(3) |
| (4) |
Το πρόβλημα που θα αντιμετωπίσουμε εδώ
είναι η επίλυση γραμμικών συστημάτων,
δηλαδή ο προσδιορισμός του άγνωστου διανύσματος ![]() , δεδομένου του
πίνακα
, δεδομένου του
πίνακα ![]() , ο οποίος λέγεται πίνακας του συστήματος,
και του διανύσματος των σταθερών όρων,
, ο οποίος λέγεται πίνακας του συστήματος,
και του διανύσματος των σταθερών όρων, ![]() .
(Θα περιοριστούμε σε συστήματα στα οποία ο
.
(Θα περιοριστούμε σε συστήματα στα οποία ο ![]() είναι τετραγωνικός πίνακας,
δηλαδή συστήματα με ίσο αριθμό εξισώσεων και αγνώστων.)
είναι τετραγωνικός πίνακας,
δηλαδή συστήματα με ίσο αριθμό εξισώσεων και αγνώστων.)
Για την επίλυση γραμμικών συστημάτων υπάρχουν αρκετές διαφορετικές μέθοδοι. Εδώ θα περιγράψουμε τις πιο ευρέως χρησιμοποιούμενες: Τη μέθοδο απλής αντικατάστασης, τη μέθοδο ευθείας αντιστροφής, τη μέθοδο του Cramer, την απαλοιφή Gauss και την τριγωνική παραγοντοποίηση ή παραγοντοποίηση LU. Το ποια επό τις μεθόδους αυτές είναι προσφορότερη εξαρτάται από το μέγεθος και τη μορφή του κάθε συγκεκριμμένου συστήματος. Επιπλέον, υπάρχει η δυνατότητα το γραμμικό σύστημα να μην έχει καμία λύση (στο παράδειγμα του συστήματος (3) αυτό θα συνέβαινε αν οι ευθείες ήταν παράλληλες) ή να έχει άπειρες λύσεις (στο παράδειγμα του συστήματος (3) αν οι οι ευθείες ταυτίζονταν).
Για να περιγράψουμε τους τρόπους επίλυσης
γραμμικών συστημάτων και τις συνθήκες ύπαρξης λύσης
θα θεωρήσουμε το πιο γενικό σύστημα ![]() ,
,
| (5) |
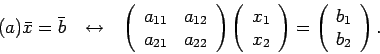 |
(6) |
1. Απλή αντικατάσταση
Είναι η απλούστερη σε ιδέα από τις μεθόδους. Πρώτο βήμα είναι
η επίλυση
κάποιας από τις εξισώσεις του συστήματος ως προς έναν άγνωστο
και η αντικατάσταση
του αγνώστου αυτού στις άλλες εξισώσεις.
Προκύπτει έτσι ένα σύστημα
μικρότερο από το αρχικό κατά μία εξίσωση και έναν άγνωστο,
στο οποίο επαναλαμβάνεται η παραπάνω
διαδικασία, κ.ο.κ., με τελικό αποτέλεσμα μία απλή εξίσωση,
ενός αγνώστου. Υπολογίζοντας τον άγνωστο αυτόν, τα βήματα στη συνέχεια
μπορούν να ακολουθηθούν αντίστροφα, αντικαθιστώντας το αποτέλεσμα στις
άλλες εξισώσεις και υπολογίζοντας έτσι και τους υπόλοιπους
αγνώστους.
Π.χ., για το σύστημα (5) το πρώτο βήμα της αντικατάστασης δίνει
| (7) |
2. Μέθοδος ευθείας αντιστροφής
Η μέθοδος αυτή συνίσταται στον πολλαπλασιασμό και των δύο μελών της
εξίσωσης
![]() με τον αντίστροφο του πίνακα
με τον αντίστροφο του πίνακα ![]() ,
τον
,
τον ![]() .
Για να μπορεί να γίνει αυτό θα πρέπει ο
.
Για να μπορεί να γίνει αυτό θα πρέπει ο ![]() να είναι αντιστρέψιμος,
ή, ισοδύναμα, η ορίζουσά του να είναι διαφορετική από
μηδέν (
να είναι αντιστρέψιμος,
ή, ισοδύναμα, η ορίζουσά του να είναι διαφορετική από
μηδέν (
![]() ).
Τότε έχουμε
).
Τότε έχουμε
| (8) |
Αν το διάνυσμα ![]() είναι μηδέν τότε η μόνη λύση του συστήματος
είναι η μηδενική.
είναι μηδέν τότε η μόνη λύση του συστήματος
είναι η μηδενική.
Αν η ορίζουσα του ![]() είναι μηδέν, το σύστημα είτε δεν έχει λύση
ή έχει άπειρες λύσεις.
είναι μηδέν, το σύστημα είτε δεν έχει λύση
ή έχει άπειρες λύσεις.
Λόγω της εμπλοκής πολλών πράξεων στη διαδικασία εύρεσης του αντιστρόφου,
η μέθοδος ευθείας αντιστροφής δεν προσφέρεται για την επίλυση
μεγάλων συστημάτων.
Τα βασικά της πλεονεκτήματα είναι ότι προσφερεται
για την περίπτωση όπου χρειάζεται η επίλυση πολλών
συστημάτων με τον ίδιο πίνακα ![]() αλλά διαφορετικό
δεξιό διάνυσμα
αλλά διαφορετικό
δεξιό διάνυσμα ![]() , καθώς και το ότι βοηθά να εξαχθούν οι συνθήκες
επιλυσιμότητας των γραμμικών συστημάτων.
, καθώς και το ότι βοηθά να εξαχθούν οι συνθήκες
επιλυσιμότητας των γραμμικών συστημάτων.
3. Μέθοδος του Cramer ή των οριζουσών
Μια άλλη μέθοδος χρήσιμη για την επίλυση σχετικά μικρών συστημάτων
καθώς και γαι τη διερεύνηση τέτοιων συστημάτων είναι η μέθοδος του Cramer
ή των οριζουσών, η οποία δίνει τους αγνώστους του συστήματος
ως πηλίκα δύο οριζουσών.
Στη συνέχεια παρουσιάζουμε και επεξηγούμε τη μέθοδο αυτή, χρησιμοποιώντας
το σύστημα (6).
Έστω ο πίνακας ![]() του συστήματος (6),
με
του συστήματος (6),
με
![]() . Πολλαπλασιάζοντας επί
. Πολλαπλασιάζοντας επί
![]() την ορίζουσα του πίνακα
αυτού παίρνουμε
την ορίζουσα του πίνακα
αυτού παίρνουμε
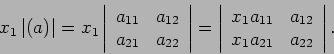 |
(9) |
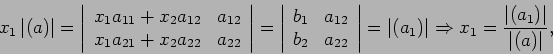 |
(10) |
Γενικά, για σύστημα ![]() εξισώσεων με
εξισώσεων με ![]() αγνώστους
αγνώστους
 |
(11) |
Συνθήκες επιλυσιμότητας γραμμικών συστημάτων: Mε οδηγό την Εξ. (8), το γεωμετρικό παράδειγμα (3) και τις εξισώσεις (11) συμπεραίνουμε τα εξής:
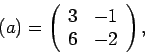
Άπειρες λύσεις έχουμε στην περίπτωση που
το διάνυσμα ![]() :
(i) είτε είναι μηδέν,
(ii) είτε παίρνει
κάποιες άλλες συγκεκριμμένες
τιμές, π.χ., εδώ,
:
(i) είτε είναι μηδέν,
(ii) είτε παίρνει
κάποιες άλλες συγκεκριμμένες
τιμές, π.χ., εδώ,
![]() .
Η περίπτωση (i) για τον πιο πάνω πίνακα
.
Η περίπτωση (i) για τον πιο πάνω πίνακα ![]() θα σήμαινε
σύστημα
της μορφής
θα σήμαινε
σύστημα
της μορφής
![]() και
και
![]() . Λύση τότε θα είναι όλα τα
. Λύση τότε θα είναι όλα τα ![]() και
και ![]() που ικανοποιούν την
που ικανοποιούν την ![]() , δηλαδή
κάθε διάνυσμα
, δηλαδή
κάθε διάνυσμα

Σε αυτές τις περιπτώσεις, (i) και (ii), οι ορίζουσες
Cramer του συστήματος είναι όλες ίσες με
μηδέν. Δηλαδή, ένα γραμμικό σύστημα με
![]() έχει άπειρες
λύσεις στην περίπτωση
που οι ορίζουσες
Cramer του είναι όλες ίσες με μηδέν.
έχει άπειρες
λύσεις στην περίπτωση
που οι ορίζουσες
Cramer του είναι όλες ίσες με μηδέν.
Αν κάποια από τις ορίζουσες Cramer είναι μη μηδενική το σύστημα δεν έχει καμία λύση, ή, όπως συχνά λέγεται, είναι αδύνατον.
Συνοψίζοντας τα παραπάνω, θα μπορούσαμε να πούμε ότι σε γραμμικά συστήματα υπάρχουν οι εξής δυνατότητες, όσον αφορά την ύπαρξη λύσης:
Για την ειδική περίπτωση των ομογενών γραμμικών συστημάτων, δηλαδή των
συστημάτων της μορφής ![]() , η οποία συναντάται
πολύ συχνά σε εφαρμογές, οι συνθήκες επιλυσιμότητας,
οι οποίες αναφέρθηκαν στην
προηγούμενη παράγραφο, μεταφράζονται ως εξής:
, η οποία συναντάται
πολύ συχνά σε εφαρμογές, οι συνθήκες επιλυσιμότητας,
οι οποίες αναφέρθηκαν στην
προηγούμενη παράγραφο, μεταφράζονται ως εξής:
Χρησιμοποιήστε τις συνθήκες επιλυσιμότητας γραμμικών συστημάτων για να αιτιολογήσετε (i) γιατί ένα ομογενές σύστημα δεν είναι ποτέ αδύνατον, (ii) γιατί η μόνη περίπτωση για να έχει ένα ομογενές σύστημα μη μηδενικές λύσεις είναι η ορίζουσα του πίνακά του να είναι ίση με μηδέν.
4. Απαλοιφή Gauss
Η διαδικασία της επίλυσης συστημάτων με απαλοιφή Gauss συνίσταται στην πρόσθεση σε κάθε γραμμή κατάλληλων πολλαπλασίων μιας άλλης γραμμής, ώστε το σύστημα να οδηγηθεί σε απλούστερο ισοδύναμο σύστημα. Αυτό συνήθως γίνεται με κάπως συστηματικό τρόπο (ιδιαίτερα στην επίλυση συστημάτων μέσω υπλογιστή): Ξεκινάμε από την πρώτη γραμμή, την οποία πολλαπλασιάζουμε κατάλληλα και την προσθέτουμε στις επόμενες, ώστε να μηδενιστεί ο συντελεστής του πρώτου αγνώστου. Συνεχίζουμε την ίδια διαδικασία με τη δεύτερη γραμμή, την οποία επίσης πολλαπλασιάζουμε κατάλληλα και την προσθέτουμε στις επόμενες, κ.ο.κ. Ο στόχος είναι να καταλήξουμε σε ένα τριγωνικό σύστημα, το οποίο μπορεί να λυθεί πολύ εύκολα με αντικατάσταση.
Θα παρουσιάσουμε αναλυτικότερα την παραπάνω διαδικασία, χρησιμοποιώντας ένα
συγκεκριμμένο σύστημα ![]() .
Έστω το σύστημα
.
Έστω το σύστημα
| (12) | |||
| (13) | |||
| (14) | |||
Τα βήματα που περιγράφονται στις (12)-(14) συνήθως εκφράζονται
σε πιο συμπαγή
μορφή, χρησιμοποιώντας πίνακες:
Κατασκευάζουμε τον επαυξημένο πίνακα του συστήματος, δηλαδή
τον πίνακα που περιέχει τον πίνακα του συστήματος με μία επιπλέον στήλη,
αυτή του δεξιού μέλους. Τα βήματα (12)-(14) τότε περιγράφονται ως εξής:
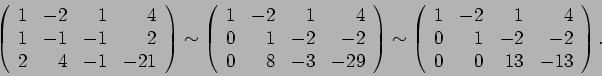 |
(15) |
Η μέθοδος της απαλοιφής προσφέρεται για την επίλυση μεγάλων αλγεβρικών συστημάτων και χρησιμοποιείται από πολλά υπολογιστικά προγράμματα επίλυσης γραμμικών συστημάτων.
5. Τριγωνική παραγοντοποίηση ή παραγοντοποίηση LU
Μια άλλη μέθοδος που επίσης προσφέρεται για την υπολογιστική επίλυση γραμμικών
συστημάτων
είναι η τριγωνική παραγοντοποίηση.
Κατά τη μέθοδο αυτή ο πίνακας του συστήματος γράφεται ως γινόμενο
ενός κάτω τριγωνικού πίνακα, (![]() ) (από το lower triangular),
και ενός άνω τριγωνικού πίνακα, (
) (από το lower triangular),
και ενός άνω τριγωνικού πίνακα, (![]() ) (από το upper triangular):
) (από το upper triangular):
| (16) |
Π.χ., για το σύστημα (6),
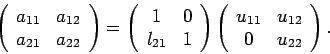 |
(17) |
Το γραμμικό σύστημα
![]() , τότε, παίρνει τη μορφή
, τότε, παίρνει τη μορφή
![]() . Θέτοντας
. Θέτοντας
![]() η επίλυση του
αρχικού συστήματος
ανάγεται στην επίλυση των δύο συστημάτων
η επίλυση του
αρχικού συστήματος
ανάγεται στην επίλυση των δύο συστημάτων
| (18) |