Τελεστές και πίνακες

1. Τελεστές και πίνακες – Γενικά

Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο.

Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα άλλο (του ίδιου ή άλλου διανυσματικού χώρου).

Τ|x>=|y>                 (1)

(Στην (1) ο τελεστής Τ δρα πάνω στο διάνυσμα |x> και το στέλνει (απεικονίζει, μετασχηματίζει) στο διάνυσμα |y>)

Παράδειγμα πολύ απλού τελεστή είναι ο  Τ=a (a μιγαδικός). Η δράση του πάνω σε ένα διάνυσμα αντιστοιχεί σε πολλαπλασιασμό του διανύσματος με τον αριθμό a.

Άλλο παράδειγμα τελεστή είναι ο τελεστής στροφής, η δράση του οποίου πάνω σε ένα διάνυσμα προκαλεί τη στροφή του διανύσματος κατά ορισμένη γωνία. (Γενικά, οποιοσδήποτε μετασχηματισμός διανυσμάτων – π.χ. στροφή, επιμήκυνση, μεταφορά - μπορεί να θεωρηθεί αποτέλεσμα της δράσης κάποιου τελεστή.)

Άλλο παράδειγμα τελεστή (ο οποίος δρα σε διανυσματικό χώρο συναρτήσεων) είναι η παράγωγος d/dx. Η δράση του πάνω σε συνάρτηση είναι η παραγώγισή της.

Ένας τελεστής Τ λέγεται γραμμικός αν για οποιαδήποτε διανύσματα |x>, |y> του διανυσματικού χώρου στον οποίο δρα ο τελεστής, και για κάθε αριθμούς λ, m (πραγματικούς ή μιγαδικούς) ισχύει

Τ(λ|x>+m|y>)= λ(T|x>)+m(T|y>)

Είναι η παράγωγος γραμμικός τελεστής;

Αν Τ₁, Τ₂ γραμμικοί τελεστές, τότε ισχύουν οι ακόλουθες ιδιότητες:

• (Τ₁+T₂)|x>=T₁|x>+T₂|x>
• (λΤ₁)|x>=λ(T₁|x>)
• (Τ₁T₂)|x>=T₁(T₂|x>)

Σε κάθε διανυσματικό χώρο μπορούμε να ορίσουμε τον μηδενικό τελεστή Τ=0, ώστε 0|x>=0 για κάθε |x>, και τον μοναδιαίο τελεστή Τ=I, ώστε Ι|x>=|x>  για κάθε |x>.  Επίσης, για κάποιους τελεστές Τ  υπάρχει τελεστής Τ^-1, ώστε  (ΤΤ^-1) =(Τ^-1Τ)||x>=|x>. Ο  Τ^-1 λέγεται αντίστροφος του τελεστή Τ.

Γνώση ενός τελεστή σημαίνει να ξέρουμε το αποτέλεσμα της δράσης του πάνω σε οποιοδήποτε διάνυσμα του διανυσματικού χώρου. Αν έχουμε τον τελεστή σε «κλειστή» μορφή, όπως  ο τελεστής της παραγώγου, αυτό είναι εύκολο. Συνήθως, όμως, σε μη συναρτησιακούς διανυσματικούς χώρους δεν μπορούμε να έχουμε τους τελεστές σε τέτοια μορφή.

Σε τέτοιες περιπτώσεις είναι εύκολο να δειχθεί ότι για να ξέρουμε τη δράση του τελεστή πάνω σε οποιοδήποτε διάνυσμα |x> αρκεί να ξέρουμε τη δράση του πάνω στα διανύσματα κάποιας βάσης του διανυσματικού χώρου:

Δηλαδή αν ξέρουμε το Τ|e_i> για κάθε  |e_i>, τότε γνωρίζουμε το |y> =Τ|x>

Αλλά

Άρα για να ξέρουμε τη δράση του τελεστή αρκεί να ξέρουμε τους αριθμούς τ_ji, οι οποίοι λέγονται συνιστώσες του τελεστή Τ στη βάση {|e_i>}. Παρατηρήστε ότι

Οι τ_ji αποτελούν μια διδιάστατη διάταξη αριθμών, η οποία ονομάζεται πίνακας και γράφεται συνήθως στη μορφή

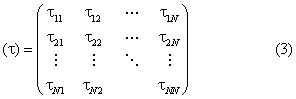
Ο (τ), με στοιχεία (τ)_ij=τ_ij λέμε ότι είναι ο πίνακας που αναπαριστά τον τελεστή Τ στη βάση {|e_i>} (με την ίδια έννοια που μια στήλη αριθμών (οι συντεταγμένες) αναπαριστάνει ένα διάνυσμα). Προσέξτε: Αλλάζοντας τη βάση αλλάζουν οι αριθμοί τ_ij.

Ο (τ) της εξ. (1) λέμε ότι είναι πίνακας Ν×Ν, δηλαδή πίνακας με Ν γραμμές και Ν στήλες. Είναι δυνατόν να έχουμε και πίνακες με διαφορετικό αριθμό γραμμών και στηλών (Ν×Μ, δηλ. Ν γραμμές, Μ στήλες – προέρχονται από μετασχηματισμούς διανυσμάτων μεταξύ διαφορετικών διανυσματικών χώρων). Οι πίνακες με ίσο αριθμό γραμμών και στηλών λέγονται τετραγωνικοί πίνακες.

Τέλος, και τα διανύσματα μπορούν να θεωρηθούν ως πίνακες, με μία μόνο στήλη (πίνακες Ν×1 ή πίνακες στήλης). Π.χ

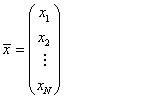
Από τα παραπάνω συμπεραίνουμε ότι αν έχουμε έναν διανυσματικό χώρο στον οποίο έχει οριστεί μια βάση, η άλγεβρα τελεστών μπορεί να αναχθεί σε άλγεβρα πινάκων, η οποία είναι και το θέμα των επόμενων εδαφίων.

2. Πράξεις πινάκων

Οι πράξεις μεταξύ πινάκων μπορούν να προκύψουν εύκολα από τις ιδιότητες των τελεστών τους οποίους εκπροσωπούν οι πίνακες.

Στα παρακάτω, το σύμβολο (α)_ij=α_ij θα συμβολίζει το στοιχείο του πίνακα (α) που βρίσκεται στην i γραμμή και στην j στήλη.

Πριν να αναφερθούμε στις πράξεις μεταξύ πινάκων θα ορίσουμε την ισότητα πινάκων.

Δύο πίνακες θα λέμε ότι είναι ίσοι αν τα στοιχεία τους είναι ένα προς ένα ίσα, δηλ

(α)=(b) αν και μόνο αν α_ij=b_ij για κάθε i,j

Πράξεις πινάκων:

Άθροισμα πινάκων: ((α)+(b))_ij=α_ij+b_ij, δηλ.

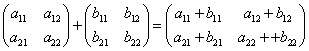
Ιδιότητες:

• (α)+(b)=(b)+(α) (αντιμεταθετική),
• (α)+[(b)+(c)]=[(α)+(b)]+(c) (προσαιτεριστική)

Πολλαπλασιασμός πίνακα με αριθμό:

Προκύπτει ένας νέος πίνακας, με στοιχεία (λ(α))_ij=λα_ij, δηλ.

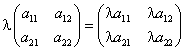
Ιδιότητες:

• λ[(α)+(b)]=λ(α)+λ(b)
• (λ+m)(α)=λ(α)+m(α)
• (λm)(α)=λ(m(α))      (λ, m αριθμοί)

Πολλαπλασιασμός πίνακα με διάνυσμα:

Το αποτέλεσμα είναι ένα νέο διάνυσμα (σκεφτείτε τη δράση του αντίστοιχου τελεστή πάνω σε διάνυσμα), με συνιστώσες  [(α)x]_i=∑_j α_ij x_j (δείτε την πιο πάνω εξ. (2)), δηλ.

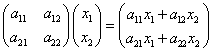
Πολλαπλασιασμός πινάκων: Αν έχουμε δύο πίνακες (α) και (b), το γινόμενο (α)(b) υπάρχει μόνο αν ο αριθμός των στηλών του (α) ισούται με τον αριθμό των γραμμών του (b). Αν ο (α) είναι πίνακας Ν×Μ και ο (b) πίνακας M×Κ, το γινόμενο (γ)=(α)(b) είναι πίνακας Ν×Κ, με στοιχεία

(γ)_ij =((α)(b))_ij=∑_k α_ik b_kj,

δηλαδή

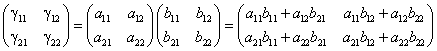
(δηλ. το ij στοιχείο του γινομένου είναι εσωτερικό γινόμενο της γραμμής i του (α)  με τη στήλη  j του (b)).

Ιδιότητες:

• [(α)+(b)](c)=(α)(c)+(b)(c)
• [(α)(b)](c)=(α)[(b)(c)]
• (c)[(α)+(b)]=(c)(α)+(c)(b)
• Προσοχή! δεν ισχύει η αντιμεταθετική ιδιότητα, δηλ. (α)(b)≠(b)(α)

3.   Ειδικές, χρήσιμες κατηγορίες πινάκων

Παρακάτω αναφέρουμε μερικές ειδικές κατηγορίες πινάκων, τους οποίους συναντάμε συχνά σε εφαρμογές.

Μηδενικός πίνακας (0) (αντιστοιχεί στον μηδενικό τελεστή) είναι ο πίνακας για τον οποίο ισχύει

(0)(α)= (α)(0)=(0) για κάθε (α).

Ένας μηδενικός πίνακας έχει όλα του τα στοιχεία του ίσα με μηδέν.

Μοναδιαίος ή ταυτοτικός πίνακας (ε) (αντιστοιχεί στον μοναδιαίο τελεστή) είναι ο πίνακας για τον οποίο ισχύει

 (ε)(α)=(α)(ε)=(α) για κάθε (α).

Ο ταυτοτικός πίνακας έχει όλα του τα στοιχεία ίσα με μηδέν, εκτός από τα στοιχεία της κύριας διαγωνίου, τα οποία είναι μονάδα. Π.χ ο μοναδιαίος 2×2 είναι ο

Διαγώνιος λέγεται ένας  πίνακας (δ) ο οποίος έχει όλα του τα στοιχεία ίσα με μηδέν, εκτός από τα στοιχεία της κύριας διαγωνίου, δηλαδή τα στοιχεία δ_ij με  i=j, π.χ.

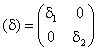
Άνω (κάτω) τριγωνικός λέγεται ένας πίνακας στον οποίο είναι μη μηδενικά μόνο τα στοιχεία πάνω (κάτω) από την κύρια διαγώνιο, καθώς και αυτά της κύριας διαγωνίου. Π.χ.

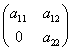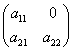 (άνω τριγωνικός),                             (κάτω τριγωνικός)

Τριδιαγώνιος λέγεται ο πίνακας στον οποίο είναι μη μηδενικά μόνο τα στοιχεία της κύριας διαγωνίου και της διαγωνίου πάνω και κάτω από την κύρια. Π.χ.

, δηλ. α_ij≠0 αν i=j, j±1.

Έστω ο πίνακας (α) με στοιχεία (a)_ij=a_ij, πχ.

.

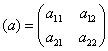Συζυγής του πίνακα  (α) λέγεται ο πίνακας που έχει στοιχεία του τα μιγαδικά συζυγή των στοιχείων του (α). Θα τον συμβολίζουμε με (α*). Δηλ (α*)_ij=(α_ij)* ή

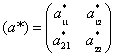
Αν ο πίνακας (α) είναι πραγματικός, τότε (α*)=(α).

Ανάστροφος του πίνακα  (α) λέγεται ο πίνακας που έχει γραμμές τις στήλες του (α) και στήλες τις γραμμές του (α). Θα τον συμβολίζουμε με (α)^Τ, δηλ.

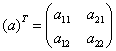
Αν ένας πίνακας ισούται με τον ανάστροφό του, τότε ο πίνακας λέγεται συμμετρικός. Αν (α) συμμετρικός, τότε α_ij=α_ji. Π.χ.

Ερμιτιανός συζυγής ή προσαρτημένος του πίνακα  (α) λέγεται ο ανάστροφος του συζυγούς τού (α) (ή ο συζυγής του αναστρόφου του (α)). Θα τον συμβολίζουμε με (α)⁺. Δηλ. (α)⁺ =(α*)^Τ. Π.χ.

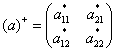
Αν ένας πίνακας (α) ισούται με τον προσαρτημένο του τότε ο (α) λέγεται ερμιτιανός ή αυτοπροσαρτημένος πίνακας. Για έναν αυτοπροσαρτημένο πίνακα (α) ισχύει α_ij=(α_ji)*. Οι αυτοπροσαρτημένοι πίνακες αποτελούν μια από τις πιο χρήσιμες κατηγορίες πινάκων. Παράδειγμα 2×2 ερμιτιανού πίνακα:

Αν ένας πίνακας μετατίθεται με τον ερμιτιανό συζυγή του, δηλ. (α)(α)⁺=(α)⁺(α) ο πίνακας αυτός λέγεται κανονικός. Π.χ.

Αντίστροφος του πίνακα  (α), αν υπάρχει, λέγεται ο πίνακας (α)^-1, τέτοιος ώστε  

(α) (α)^-1 =(α)^-1 (α)=(ε) (ο μοναδιαίος πίνακας).  Για τον υπολογισμό του αντιστρόφου ενός πίνακα θα μιλήσουμε σε επόμενο εδάφιο.

Αν για έναν πίνακα (α) ο οποίος έχει αντίστροφο ισχύει (α)⁺=(α)^-1, τότε ο (α) λέγεται μοναδιακός πίνακας. Πολλές φορές συμβολίζεται με (u) (από το unitary). Προσοχή: Να μην συγχέεται με τον μοναδιαίο!

Αν για έναν πίνακα (α) ο οποίος έχει αντίστροφο ισχύει (α)^Τ=(α)^-1, τότε ο (α) λέγεται ορθογώνιος πίνακας. Πολλές φορές συμβολίζεται με (ο) (από το orthogonal).

Για πίνακες με πραγματικά στοιχεία, όπου  (α)⁺ =(α)^Τ, ο μοναδιακός και ο ορθογώνιος πίνακας ταυτίζονται.

Οι μοναδιακοί και οι ορθογώνιοι πίνακες αποτελούν από τις πιο χρήσιμες κατηγορίες πινάκων. Η ορίζουσά τους έχει μέτρο μονάδα, οι στήλες τους αποτελούν ορθοκανονικό σύστημα διανυσμάτων και όταν πολλαπλασιάσουν ένα διάνυσμα οδηγούν σε διάνυσμα με το ίδιο μήκος (μέτρο) με το αρχικό. Αποτελούν επίσης ειδικές κατηγορίες κανονικών πινάκων.

4.     Ίχνος και ορίζουσα πίνακα

Το ίχνος και η ορίζουσα είναι δύο χρήσιμοι αριθμοί, χαρακτηριστικοί κάθε πίνακα. Ορίζονται μόνο για τετραγωνικούς πίνακες

Ίχνος πίνακα, Tr  (από το trace)  ονομάζουμε το άθροισμα των διαγώνιων στοιχείων του πίνακα:

Tr(α)=∑_iα_ii,

Δηλ.

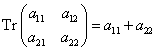
Για το ίχνος ισχύουν:

• Tr((α)+(b))=Tr(α)+Tr(b)
• Tr((α)(b))=Tr((b)(α)) (ακόμα και αν (α)(b)≠(b)(α))

Αξίζει να σημειωθεί επίσης ότι το ίχνος είναι χαρακτηριστικό του τελεστή τον οποίο εκπροσωπεί ο πίνακας και παραμένει το ίδιο για κάθε αναπαράσταση του τελεστή.

Ορίζουσα πίνακα είναι ένας αριθμός, ο οποίος υπολογίζεται από τα στοιχεία του πίνακα (με προσθέσεις και πολλαπλασιασμούς των στοιχείων αυτών). Η ορίζουσα ενός πίνακα, π.χ.

,

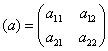συμβολίζεται είτε με det(α) (από την αγγλική λέξη  determinant=ορίζουσα) είτε ως

.

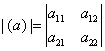Πριν αναφερθούμε στον τρόπο υπολογισμού της ορίζουσας θα εισάγουμε την έννοια του υποπίνακα, της υποορίζουσας και του αλγεβρικού συμπληρώματος πίνακα.

Υποπίνακας (c_ij) του πίνακα (α) ονομάζεται ο πίνακας που προκύπτει από τον (α) με απαλοιφή της γραμμής i και της στήλης j.  Π.χ. ο (c₁₁) του πιο πάνω πίνακα (α) είναι το στοιχείο α₂₂  (πίνακας 1×1). Οι ορίζουσες τέτοιων υποπινάκων του (α) ονομάζονται υποορίζουσες του πίνακα (α).

Αλγεβρικό συμπλήρωμα του υποπίνακα (c_ij) λέγεται ο αριθμός Δ_ij=(-1)^i+j det(c_ij)

Χρησιμοποιώντας τα παραπάνω, η ορίζουσα ενός πίνακα (α) υπολογίζεται ως εξής:

det(α)=∑_jα_ijΔ_ij =∑_j(-1)^i+j α_ij det(c_ij) ή     det(α)= ∑_iα_ijΔ_ij =∑_i(-1)^i+j α_ij det(c_ij)      ₍₁₎

Ο δείκτης j μετράει τις στήλες του πίνακα (α) και ο δείκτης i τις γραμμές του. Στο άθροισμα ως προς j ο δείκτης i μπορεί να δηλώνει οποιαδήποτε γραμμή του πίνακα. Λέμε τότε ότι υπολογίζουμε την ορίζουσα με ανάπτυγμα ως προς τη γραμμή i. Οποιαδήποτε από τις γραμμές του πίνακα αν επιλεγεί το αποτέλεσμα θα είναι το ίδιο. Ανάλογα και για το άθροισμα ως προς i. Τότε λέμε ότι υπολογίζουμε την ορίζουσα με ανάπτυγμα ως προς τη στήλη j.

Τα παραπάνω θα γίνουν περισσότερο κατανοητά με ένα συγκεκριμένο παράδειγμα: Έστω ο πίνακας.

.

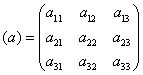Θα υπολογίσουμε την ορίζουσά του αναπτύσσοντας ως προς την πρώτη γραμμή, δηλ. χρησιμοποιώντας τη σχέση det(α)= ∑_j (-1)^i+j α_ij det(c_ij) , με i=1. Δηλ.

det(α)= (-1)¹⁺¹ α₁₁ det(c₁₁) +(-1)¹⁺² α₁₂ det(c₁₂) +(-1)¹⁺³ α₁₃ det(c₁₃),

ή, πιο παραστατικά,

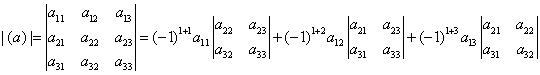
Ο υπολογισμός γίνεται ευκολότερος στην πράξη αντιστοιχίζοντας στο στοιχείο α₁₁ το πρόσημο + και στα άλλα στοιχεία εναλλάξ πρόσημο + ή -, και αναπτύσσοντας ως προς κάποια γραμμή ή στήλη χρησιμοποιώντας τα πρόσημα αυτά. Π.χ. στο πιο πάνω παράδειγμα 3×3 πίνακα, όπου αναπτύσσουμε ως προς την πρώτη γραμμή,

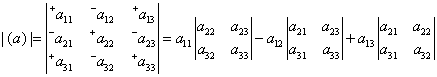
Αν ο (α) είναι πίνακας 2×2 ο υπολογισμός είναι πολύ απλός:

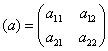,   τότε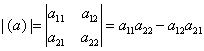   

Επίσης, ειδικά για 3×3 πίνακες, υπάρχει και ένας ευκολότερος τρόπος υπολογισμού, γνωστός ως κανόνας του Sarrus:

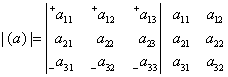
Το εξωτερικό γινόμενο διανυσμάτων του γνωστού μας τριδιάστατου ευκλείδιου χώρου, μπορεί να υπολογιστεί εύκολα με χρήση οριζουσών, ως (σε καρτεσιανές συντεταγμένες)

.

Υπολογίστε την ορίζουσα ενός διαγώνιου πίνακα 3×3.

Υπολογίστε την ορίζουσα ενός κάτω τριγωνικού πίνακα 3×3.

5. Ιδιότητες οριζουσών

Για να μπορέσουμε να παρουσιάσουμε σε πιο συμπαγή μορφή τις ιδιότητες των οριζουσών, θα γράψουμε τον πίνακα (a) στην  εξής μορφή:

όπου το α_i με την παύλα δηλώνει την i στήλη του (α).

1.   (κοινός παράγων μιας στήλης ή γραμμής βγαίνει κοινός παράγων της ορίζουσας).

2. Αν μια γραμμή ή στήλη μιας ορίζουσας είναι μηδέν η ορίζουσα είναι ίση με μηδέν (προκύπτει αμέσως από την 1).

3. Η ορίζουσα του διαγώνιου πίνακα είναι γινόμενο των διαγώνιων στοιχειών του πίνακα. Η ορίζουσα του ταυτοτικού πίνακα είναι ίση με 1.

4. Αντιμεταθέτοντας δύο οποιεσδήποτε γραμμές ή στήλες μιας ορίζουσας η ορίζουσα αλλάζει πρόσημο, δηλ.  (οι γραμμές (ή οι στήλες) δεν είναι απαραίτητο να είναι γειτονικές).

5. Όταν δύο γραμμές ή στήλες μιας ορίζουσας είναι ίσες ή ανάλογες, η ορίζουσα είναι μηδέν, δηλ. . ( (από 1) και  (από 4)).

6. , δηλ. όταν μια γραμμή ή στήλη μιας ορίζουσας γράφεται ως άθροισμα δύο προσθετέων, η ορίζουσα μπορεί να σπάσει σε άθροισμα δύο οριζουσών (προκύπτει εύκολα από τον τύπο (1), αναπτύσσοντας ως προς τη γραμμή ή στήλη που είναι άθροισμα).

7. Αν προστεθεί σε μια γραμμή (ή στήλη) μιας ορίζουσας το πολλαπλάσιο μιας άλλης γραμμής (ή στήλης), η ορίζουσα παραμένει αμετάβλητη, δηλ.  (προκύπτει εύκολα από την ιδιότητα 6, σε συνδυασμό με την 5). 

8. Η ορίζουσα του γινομένου πινάκων ισούται με το γινόμενο των οριζουσών των πινάκων αυτών, δηλ. . Αν ο (β) είναι ο αντίστροφος του (α), τότε .

9. (προκύπτει εύκολα αναπτύσσοντας τον έναν πίνακα ως προς γραμμές και τον άλλον ως προς στήλες).   (αφού ).

10.  Αν η ορίζουσα ενός πίνακα (α) είναι μηδέν τότε οι στήλες του (α) είναι γραμμικά εξαρτημένα διανύσματα. Αν είναι διαφορετική από μηδέν οι στήλες είναι διανύσματα γραμμικά ανεξάρτητα. Το ίδιο ισχύει και για τις γραμμές του (α).

6. Τάξη πίνακα, αντίστροφος πίνακα

Τάξη πίνακα: Τάξη ενός πίνακα (α) λέγεται ο αριθμός των γραμμικά ανεξάρτητων στηλών (ή γραμμών) του (α).

Χρησιμοποιώντας την παραπάνω ιδιότητα 10 των οριζουσών, μπορεί να δειχθεί ότι αν ο (α) είναι τετραγωνικός πίνακας Ν×Ν με det(a)≠0 τότε η τάξη του (α) ισούται με Ν (δηλ. με τη διάστασή του). Αν det(a)=0 η τάξη του (a) ισούται με τη διάσταση του μέγιστου τετραγωνικού υποπίνακά του με μη μηδενική ορίζουσα.

Ένας πίνακας του οποίου η ορίζουσα ισούται με μηδέν λέγεται ιδιόμορφος ή ιδιάζων πίνακας.

Αντίστροφος πίνακα: Είπαμε στα προηγούμενα ότι ο αντίστροφος ενός πίνακα (α), αν υπάρχει, ορίζεται από τη σχέση (α) (α)^-1 =(α)^-1 (α)=(ε) ((ε) είναι ο μοναδιαίος πίνακας). 

Η συνθήκη για την ύπαρξη αντιστρόφου είναι ο πίνακας (α) να έχει μη μηδενική ορίζουσα. Πίνακες με ορίζουσα ίση με μηδέν (ιδιόμορφοι πίνακες) δεν είναι αντιστρέψιμοι.

Υπολογισμός αντιστρόφου: Ο υπολογισμός του αντιστρόφου ενός πίνακα (α) σχετίζεται στενά με τον υπολογισμό της ορίζουσας του (α). Υπενθυμίζουμε ότι η ορίζουσα του πίνακα (α) δίδεται από τη σχέση det(α)= ∑_j(-1)^i+j α_ij det(c_ij) = ∑_jα_ijΔ_ij. Οι αριθμοί Δ_ij (τα αλγεβρικά συμπληρώματα των στοιχείων του (α)), οι οποίοι αποτελούν μια διαδιάστατη διάταξη αριθμών, μπορούν να γραφούν και αυτοί σε μορφή πίνακα:

.

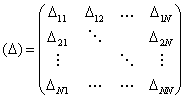Μπορεί να αποδειχθεί τότε ότι (α)(Δ)^Τ=(Δ)^Τ(α)=(ε)det(α), όπου (Δ)^Τ είναι ο ανάστροφος του (Δ) και (ε) ο μοναδιαίος. Πολλαπλασιάζοντας και τα δύο μέλη της ισότητας από αριστερά με (α)^-1 και χρησιμοποιώντας τον ορισμό του αντιστρόφου, προκύπτει εύκολα ότι

(Μπορείτε να αποδείξετε, χρησιμοποιώντας τον τύπο (1) για τον υπολογισμό της ορίζουσας, το εξής?: )

Για τον αντίστροφο πίνακα ισχύουν οι εξής ιδιότητες:

• ((α)^-1)^-1=(α)
• ((α)^Τ)^-1=((α)^-1)^Τ
• ((α)⁺)^-1=((α)^-1)⁺
• ((α)(b))^-1=(b)^-1 (α)^-1 (προσέξτε την αλλαγή στη σειρά των πινάκων).

Αποδείξτε τις παραπάνω ιδιότητες του αντιστρόφου χρησιμοποιώντας τον ορισμό του.

Αποδείξτε ότι ο αντίστροφος ενός διαγώνιου πίνακα (δ), είναι ένας διαγώνιος πίνακας με στοιχεία τα αντίστροφα των στοιχείων του (δ).

Αποδείξτε ότι ο αντίστροφος ενός γενικού διδιάστατου πίνακα (α) δίδεται από τη σχέση

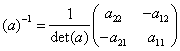
Αποδείξτε ότι η ορίζουσα ενός ορθογώνιου πίνακα είναι +1 ή -1 (χρησιμοποιήστε τον ορισμό του ορθογώνιου πίνακα, και το γεγονός ότι η det(a)^-1=1/det(a))

Αποδείξτε ότι η ορίζουσα ενός μοναδιακού πίνακα έχει μέτρο μονάδα.