Επόμενο: Ορισμός της Πιθανότητας Επάνω: p1 Προηγούμενο: Σύνθετα, στοιχειώδη και ασυμβίβαστα
Σε ό,τι ακολουθεί θα θεωρούμε ένα βασικό σύνολο ![]() το οποίο θα είναι, εν γένει, διαφορετικό
σε κάθε πρόβλημα που συναντάμε (θα είναι ο δειγματοχώρος
του συγκεκριμένου προβλήματος). Όλα τα υπόλοιπα σύνολα
θα είναι υποσύνολα του
το οποίο θα είναι, εν γένει, διαφορετικό
σε κάθε πρόβλημα που συναντάμε (θα είναι ο δειγματοχώρος
του συγκεκριμένου προβλήματος). Όλα τα υπόλοιπα σύνολα
θα είναι υποσύνολα του ![]() . Δύο υποσύνολα του
. Δύο υποσύνολα του ![]() ,
, ![]() και
και ![]() ,
λέγονται ίσα, και γράφουμε
,
λέγονται ίσα, και γράφουμε ![]() , αν
, αν ![]() και
και ![]() . Οι σημαντικότερες πράξεις συνόλων
είναι οι παρακάτω:
. Οι σημαντικότερες πράξεις συνόλων
είναι οι παρακάτω:
Δύο σύνολα ![]() και
και ![]() για τα οποία
για τα οποία
![]() λέγονται ξένα σύνολα.
λέγονται ξένα σύνολα.
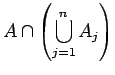 |
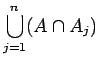 |
||
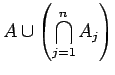 |
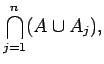 |
![]() είναι το γεγονός (που αντιστοιχεί στην πρόταση)
``ή
είναι το γεγονός (που αντιστοιχεί στην πρόταση)
``ή ![]() ή
ή ![]() ή και τα δύο'',
ή και τα δύο'',
![]() είναι το γεγονός ``και
είναι το γεγονός ``και ![]() και
και ![]() '',
'',
![]() είναι το γεγονός ``όχι
είναι το γεγονός ``όχι ![]() '', και
'', και
![]() είναι το γεγονός ``
είναι το γεγονός ``![]() αλλά όχι και
αλλά όχι και ![]() ''.
''.
Αν τα σύνολα που αντιστοιχούν στα γεγονότα ![]() και
και ![]() είναι ξένα,
τότε τα γεγονότα αυτά είναι ασυμβίβαστα.
είναι ξένα,
τότε τα γεγονότα αυτά είναι ασυμβίβαστα.
Μέχρι στιγμής περιγράψαμε πειράματα τύχης και συζητήσαμε τα
πιθανά αποτελέσματά τους ή γεγονότα. Δεν αναφέραμε
τίποτα για τη σχετική συχνότητα ή πιθανότητα εμφάνισης κάθε
αποτελέσματος, πράγμα το οποίο θα κάνουμε στο επόμενο εδάφιο.
Στο επόμενο εδάφιο, σε κάθε γεγονός ![]() θα αντιστοιχίσουμε μια αριθμητική
ποσότητα,
θα αντιστοιχίσουμε μια αριθμητική
ποσότητα, ![]() , η οποία θα κληθεί πιθανότητα του
, η οποία θα κληθεί πιθανότητα του ![]() , δηλ. πιθανότητα
να συμβεί το γεγονός
, δηλ. πιθανότητα
να συμβεί το γεγονός ![]() .
.
Maria Kafesaki 2005-05-26