Στη θεωρία, αλλά και στην πράξη, εμφανίζονται συχνά
καταστάσεις στις οποίες οι φυσιολογικές τυχαίες
μεταβλητές που πρέπει να χρησιμοποιήσουμε είναι συνεχείς και όχι
διακριτές, δηλαδή μπορούν να πάρουν οποιαδήποτε τιμή
σε ένα δεδομένο διάστημα (η τιμή αυτή και εδώ εξαρτάται προφανώς
από το αποτέλεσμα του τυχαίου πειράματος).
Τέτοια παραδείγματα είναι η τυχαία μεταβλητή, έστω 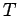 ,
που
παριστάνει το χρόνο διάσπασης ενός
ραδιενεργού σωματιδίου ή το χρόνο ζωής ενός ηλεκτρικολυ λαμπτήρα,
η τυχαία μεταβλητή
,
που
παριστάνει το χρόνο διάσπασης ενός
ραδιενεργού σωματιδίου ή το χρόνο ζωής ενός ηλεκτρικολυ λαμπτήρα,
η τυχαία μεταβλητή 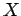 που παριστάνει
τη θέση ενός κβαντομηχανικού σωματιδίου παγιδευμένου σε μια περιοχή του χώρου,
η τυχαία μεταβλητή που παριστάνει το ύψος ενός ατόμου από ένα δεδομένο
δείγμα ατόμων, κ.ο.κ.
που παριστάνει
τη θέση ενός κβαντομηχανικού σωματιδίου παγιδευμένου σε μια περιοχή του χώρου,
η τυχαία μεταβλητή που παριστάνει το ύψος ενός ατόμου από ένα δεδομένο
δείγμα ατόμων, κ.ο.κ.
Γενικά, τυχαίες μεταβλητές που αφορούν μετρήσεις φυσικών ποσοτήτων,
όπως οι συντεταγμένες στο χώρο, το βάρος, ο χρόνος, η θερμοκρασία,
η τάση του ρεύματος, κ.τ.λ., περιγράφονται καλύτερα με συνεχείς
τυχαίες μεταβλητές.
Στην περίπτωση των συνεχών τυχαίων μεταβλητών η έκφραση
``πιθανότητα η μεταβλητή 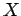 να πάρει μια ορισμένη τιμή
να πάρει μια ορισμένη τιμή
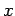 '' αντικαθίσταται από την ``πιθανότητα η μεταβλητή
'' αντικαθίσταται από την ``πιθανότητα η μεταβλητή 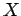 να πάρει
τιμές σε ένα ορισμένο απειροστό διάστημα γύρω από το σημείο
να πάρει
τιμές σε ένα ορισμένο απειροστό διάστημα γύρω από το σημείο
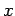 ''.
Με βάση αυτό, η συνάρτηση πυκνότητας για συνεχείς τυχαίες μεταβλητές
ορίζεται από τη σχέση
''.
Με βάση αυτό, η συνάρτηση πυκνότητας για συνεχείς τυχαίες μεταβλητές
ορίζεται από τη σχέση
Προσέξτε ότι, αντίθετα με ό,τι συμβαίνει για διακριτές
τυχαίες μεταβλητές, η τιμή της 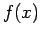 για το ενδεχόμενο
για το ενδεχόμενο 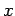 δεν είναι η πιθανότητα να συμβεί το
δεν είναι η πιθανότητα να συμβεί το 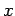 .1Αυτό που παριστάνει πιθανότητα
είναι η το γινόμενο
.1Αυτό που παριστάνει πιθανότητα
είναι η το γινόμενο 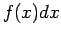 .
.
Από τον ορισμό της συνάρτησης πυκνότητας για συνεχείς κατανομές
γίνεται φανερό ότι
η πιθανότητα το αποτέλεσμα του τυχαίου πειράματος
να είναι στο διάστημα ![$[a,b]$](img92.png) δίνεται από την
δίνεται από την
(``άθροισμα'' των πιθανοτήτων όλων των απειροστών διαστημάτων 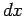 από
το
από
το 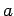 ως το
ως το 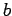 ), δηλαδή από το εμβαδόν κάτω από την
), δηλαδή από το εμβαδόν κάτω από την  στο διάστημα
στο διάστημα ![$[a,b]$](img92.png) .
.
Προφανώς, η πυκνότητα  θα είναι μια μη αρνητική συνάρτηση και
θα ικανοποιεί την
θα είναι μια μη αρνητική συνάρτηση και
θα ικανοποιεί την
αφού η ολική πιθανότητα θα πρέπει να είναι πάντα μονάδα.
Η προηγούμενη σχέση χρησιμοποιείται πολλές φορές και
ως σχέση ορισμού της συνάρτησης πυκνότητας  .
.
Στη συνέχεια, θα ορίσουμε τη συνάρτηση κατανομής για συνεχείς
τυχαίες μεταβλητές, η οποία είναι χρήσιμη για τον υπολογισμό
διαφόρων πιθανοτήτων που σχετίζονται με την τυχαία μεταβλητή 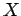 .
.
Ορισμός: Η συνάρτηση κατανομής 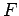 μιας τυχαίας
μεταβλητής
μιας τυχαίας
μεταβλητής 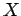 είναι η συνάρτηση
είναι η συνάρτηση
Μπορούμε εύκολα να δείξουμε ότι
Παρατηρούμε ότι για να υπολογίσουμε την πυκνότητα μιας συνεχούς
τυχαίας μεταβλητής
αρκεί να παραγωγίσουμε την 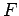 , οπότε
, οπότε
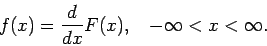
Η παραπάνω σχέση ισχύει για κάθε πραγματικό αριθμό 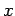 στο οποίο η
στο οποίο η 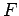 είναι συνεχής. Προφανώς, από την απαίτηση
να είναι η πιθανότητα μηδέν όταν η τυχαία μεταβλητή παίρνει
μια συγκεκριμένη τιμή, η
είναι συνεχής. Προφανώς, από την απαίτηση
να είναι η πιθανότητα μηδέν όταν η τυχαία μεταβλητή παίρνει
μια συγκεκριμένη τιμή, η 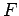 δεν μπορεί να έχει άλματα
(ασυνέχειες), άρα θα πρέπει να είναι συνεχής.
Επομένως, η
δεν μπορεί να έχει άλματα
(ασυνέχειες), άρα θα πρέπει να είναι συνεχής.
Επομένως, η 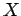 είναι συνεχής τυχαία μεταβλητή αν και μόνο
αν η
είναι συνεχής τυχαία μεταβλητή αν και μόνο
αν η 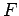 είναι συνεχής για κάθε πραγματικό αριθμό
είναι συνεχής για κάθε πραγματικό αριθμό 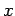 .
.
-
- Παράδειγμα 6:
Υποθέστε ότι ρίχνουμε ένα βέλος σε ένα στόχο σχήματος κυκλικού
δίσκου με κέντρο την αρχή των αξόνων Ο και ακτίνα
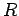 , στο επίπεδο.
Θεωρούμε ότι ο δειγματοχώρος του πειράματος είναι ομοιόμορφος,
δηλαδή η πιθανότητα να καρφωθεί το βέλος σε σημείο μιας περιοχή του
στόχου εμβαδού Ε, ορίζεται από το κλάσμα του Ε προς το συνολικό εμβαδόν
του στόχου. Αν
, στο επίπεδο.
Θεωρούμε ότι ο δειγματοχώρος του πειράματος είναι ομοιόμορφος,
δηλαδή η πιθανότητα να καρφωθεί το βέλος σε σημείο μιας περιοχή του
στόχου εμβαδού Ε, ορίζεται από το κλάσμα του Ε προς το συνολικό εμβαδόν
του στόχου. Αν 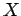 είναι η τυχαία μεταβλητή που περιγράφει
την απόσταση του σημείου που "επιλέχθηκε" από το Ο, τότε να βρεθεί
η συνάρτηση κατανομής της.
είναι η τυχαία μεταβλητή που περιγράφει
την απόσταση του σημείου που "επιλέχθηκε" από το Ο, τότε να βρεθεί
η συνάρτηση κατανομής της.
Έστω ότι το βέλος καρφώνεται σε σημείο που απέχει 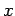 ,
,
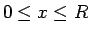 , από το Ο. Τότε, το ενδεχόμενο
, από το Ο. Τότε, το ενδεχόμενο
 (δηλαδή το
ενδεχόμενο που έχει ως σημεία τα δειγματοσημεία
(δηλαδή το
ενδεχόμενο που έχει ως σημεία τα δειγματοσημεία 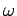 του
του
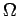 για τα οποία η τυχαία μεταβλητή
για τα οποία η τυχαία μεταβλητή 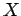 παίρνει
τιμές μικρότερες ή ίσες με
παίρνει
τιμές μικρότερες ή ίσες με 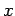 ) είναι ένας δίσκος
με κέντρο Ο και ακτίνα
) είναι ένας δίσκος
με κέντρο Ο και ακτίνα 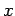 , και εμβαδόν
, και εμβαδόν  .
H πιθανότητα να πραγματοποιηθεί το
.
H πιθανότητα να πραγματοποιηθεί το  ορίζεται από την
ορίζεται από την
και η 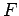 θα είναι
θα είναι
Αν
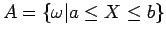 , με
, με
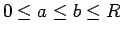 ,
τότε
,
τότε
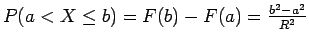 , ή
, ή
Έτσι, η πιθανότητα που αποδίδεται στο διάστημα  δεν εξαρτάται
μόνο από το μήκος του, αλλά επίσης και από το πού βρίσκεται,
αφού το
δεν εξαρτάται
μόνο από το μήκος του, αλλά επίσης και από το πού βρίσκεται,
αφού το 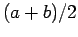 είναι το μέσο του διαστήματος
είναι το μέσο του διαστήματος ![$[a,b]$](img92.png) .
Μιλώντας χονδρικά, γεγονότα της μορφής
.
Μιλώντας χονδρικά, γεγονότα της μορφής
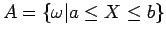 είναι πιο
πιθανά αν είναι μακριά από το κέντρο του στόχου.
είναι πιο
πιθανά αν είναι μακριά από το κέντρο του στόχου.
-
- Παράδειγμα 7: Κανονική πυκνότητα (Gauss).
Έστω η συνάρτηση
 ,
,
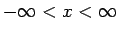 .
Υπολογίστε το
.
Υπολογίστε το 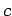 ώστε η
ώστε η  να γίνει πυκνότητα.
να γίνει πυκνότητα.
Για να κάνουμε την  πυκνότητα πρέπει να βρούμε το
πυκνότητα πρέπει να βρούμε το 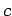 έτσι ώστε
έτσι ώστε
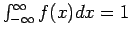 ,
Έτσι,
,
Έτσι,
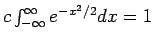 .
Το ολοκλήρωμα
.
Το ολοκλήρωμα
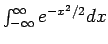 υπολογίζεται με το εξής τέχνασμα: Θέτω
υπολογίζεται με το εξής τέχνασμα: Θέτω
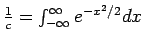 , οπότε
, οπότε
Πηγαίνοντας σε πολικές συντεταγμένες, έχουμε
Άρα,
 , και
, και
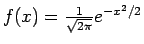 .
Η
.
Η  λέγεται τυπική κανονική πυκνότητα. Προφανώς είναι συμμετρική,
αφού
λέγεται τυπική κανονική πυκνότητα. Προφανώς είναι συμμετρική,
αφού  για κάθε
για κάθε 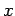 .
.
Maria Kafesaki
2007-06-08
![]() να πάρει μια ορισμένη τιμή
να πάρει μια ορισμένη τιμή
![]() '' αντικαθίσταται από την ``πιθανότητα η μεταβλητή
'' αντικαθίσταται από την ``πιθανότητα η μεταβλητή ![]() να πάρει
τιμές σε ένα ορισμένο απειροστό διάστημα γύρω από το σημείο
να πάρει
τιμές σε ένα ορισμένο απειροστό διάστημα γύρω από το σημείο
![]() ''.
Με βάση αυτό, η συνάρτηση πυκνότητας για συνεχείς τυχαίες μεταβλητές
ορίζεται από τη σχέση
''.
Με βάση αυτό, η συνάρτηση πυκνότητας για συνεχείς τυχαίες μεταβλητές
ορίζεται από τη σχέση
![]() δίνεται από την
δίνεται από την
![]() θα είναι μια μη αρνητική συνάρτηση και
θα ικανοποιεί την
θα είναι μια μη αρνητική συνάρτηση και
θα ικανοποιεί την
![]() .
.
![]() μιας τυχαίας
μεταβλητής
μιας τυχαίας
μεταβλητής ![]() είναι η συνάρτηση
είναι η συνάρτηση
![]() , οπότε
, οπότε
![]() ,
,
![]() , από το Ο. Τότε, το ενδεχόμενο
, από το Ο. Τότε, το ενδεχόμενο
![]() (δηλαδή το
ενδεχόμενο που έχει ως σημεία τα δειγματοσημεία
(δηλαδή το
ενδεχόμενο που έχει ως σημεία τα δειγματοσημεία ![]() του
του
![]() για τα οποία η τυχαία μεταβλητή
για τα οποία η τυχαία μεταβλητή ![]() παίρνει
τιμές μικρότερες ή ίσες με
παίρνει
τιμές μικρότερες ή ίσες με ![]() ) είναι ένας δίσκος
με κέντρο Ο και ακτίνα
) είναι ένας δίσκος
με κέντρο Ο και ακτίνα ![]() , και εμβαδόν
, και εμβαδόν ![]() .
H πιθανότητα να πραγματοποιηθεί το
.
H πιθανότητα να πραγματοποιηθεί το ![]() ορίζεται από την
ορίζεται από την

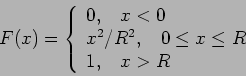
![]() πυκνότητα πρέπει να βρούμε το
πυκνότητα πρέπει να βρούμε το ![]() έτσι ώστε
έτσι ώστε
![]() ,
Έτσι,
,
Έτσι,
![]() .
Το ολοκλήρωμα
.
Το ολοκλήρωμα
![]() υπολογίζεται με το εξής τέχνασμα: Θέτω
υπολογίζεται με το εξής τέχνασμα: Θέτω
![]() , οπότε
, οπότε