Επόμενο: Ροπές, διασπορά, τυπική απόκλιση Επάνω: p3 Προηγούμενο: Συνεχείς τυχαίες μεταβλητές
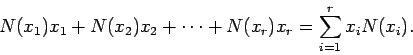
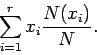
Ερμηνεύοντας την πιθανότητα ως σχετική συχνότητα, αν το ![]() είναι
αρκετά μεγάλο, περιμένουμε ότι
είναι
αρκετά μεγάλο, περιμένουμε ότι
Γενικά, έστω μια διακριτή τυχαία μεταβλητή ![]() που παίρνει τις
πεπερασμένες το πλήθος τιμές
που παίρνει τις
πεπερασμένες το πλήθος τιμές
![]() . Τότε η μέση τιμή
της
. Τότε η μέση τιμή
της ![]() , η οποια συμβολίζεται με
, η οποια συμβολίζεται με ![]() ή
ή ![]() ή
ή ![]() ή
ή ![]() είναι ο αριθμός
είναι ο αριθμός
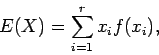
Υποθέστε ότι η ![]() έχει την ομοιόμορφη πυκνότητα
έχει την ομοιόμορφη πυκνότητα
![]() . Τότε από τον ορισμό της μέσης τιμής
έχουμε ότι
. Τότε από τον ορισμό της μέσης τιμής
έχουμε ότι
![]() ,
δηλαδή στην περίπτωση αυτή η
,
δηλαδή στην περίπτωση αυτή η ![]() είναι απλώς ο μέσος όρος των
πιθανών τιμών της
είναι απλώς ο μέσος όρος των
πιθανών τιμών της ![]() . Γενικά, όπως φαίνεται από τον ορισμό της,
η
. Γενικά, όπως φαίνεται από τον ορισμό της,
η ![]() είναι ένας "μέσος όρος" με βάρη των πιθανών τιμών της
είναι ένας "μέσος όρος" με βάρη των πιθανών τιμών της ![]() .
Όταν το πλήθος των τιμών της
.
Όταν το πλήθος των τιμών της ![]() είναι άπειρο (αριθμήσιμο),
η μέση τιμή έχει νόημα αν το άθροισμα
είναι άπειρο (αριθμήσιμο),
η μέση τιμή έχει νόημα αν το άθροισμα
![]() είναι καλά ορισμένο.
είναι καλά ορισμένο.
Για μια συνεχή τυχαία μεταβλητή με πυκνότητα ![]() η μέση τιμή
ορίζεται από τη σχέση
η μέση τιμή
ορίζεται από τη σχέση
Παρακάτω δίνονται οι σημαντικότερες ιδιότητες της μέσης τιμής,
που προκύπτουν εύκολα
από τον ορισμό της. Για δύο τυχαίες μεταβλητές
![]() και
και ![]() με πεπερασμένη μέση τιμή, έχουμε
με πεπερασμένη μέση τιμή, έχουμε
α) Αν η ![]() παίρνει μόνο μία τιμή,
παίρνει μόνο μία τιμή, ![]() σταθερά, και
σταθερά, και ![]() , τότε
, τότε ![]() .
.
β) Αν ![]() σταθερά, τότε η
σταθερά, τότε η ![]() έχει πεπερασμένη μέση τιμή,
και
έχει πεπερασμένη μέση τιμή,
και ![]() .
.
γ) Η ![]() έχει πεπερασμένη μέση τιμή και
έχει πεπερασμένη μέση τιμή και
![]()
δ) Υποθέστε ότι ![]() . Τότε,
. Τότε,
![]() .
Επιπλέον,
.
Επιπλέον, ![]() , αν και μόνο αν
, αν και μόνο αν ![]() .
.
ε)
![]()
στ)
![]() , αν
, αν ![]() και
και ![]() είναι δύο ανεξάρτητες
τυχαίες μεταβλητές.
είναι δύο ανεξάρτητες
τυχαίες μεταβλητές.
Έχουμε
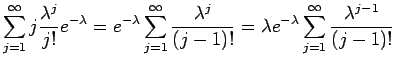 |
|||
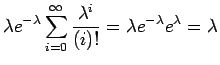 |
|||
Έχουμε
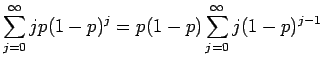 |
|||
![$\displaystyle -p(1-p) \sum_{j=0}^\infty \frac{d}{dp}[ (1-p)^j]
= -p(1-p) \frac{d}{dp} \sum_{j=0}^\infty (1-p)^j$](img160.png) |
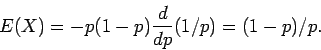
![\begin{displaymath}E(X) = \int_a^b x \frac{1}{b-a} dx
=\frac{1}{b-a} \left[ \f...
...ght]_a^b
= \frac{1}{b-a} \frac{b^2-a^2}{2} = \frac{b+a}{2} .
\end{displaymath}](img168.png)
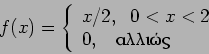
Έχουμε
![\begin{displaymath}E(X) = \int_{-\infty}^\infty x f(x) dx
= \int_0^2 x \frac{1}...
...= \frac{1}{2} \left[ \frac{x^3}{3} \right]_0^2 = \frac{4}{3} .
\end{displaymath}](img170.png)
Maria Kafesaki 2007-06-08