- 1.
- Να προσδιοριστεί η σταθερά
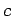 ώστε η συνάρτηση
ώστε η συνάρτηση
να είναι συνάρτηση πυκνότητας. Υπολογίστε τη συνάρτηση κατανομής
για την τυχαία μεταβλητή της οποίας η  είναι συνάρτηση πυκνότητας.
Κατόπιν υπολογίστε την
είναι συνάρτηση πυκνότητας.
Κατόπιν υπολογίστε την 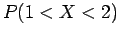 .
.
- 2.
- Ένα νόμισμα ρίχνεται τρεις φορές. Αν
η τυχαία μεταβλητή
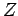 παριστάνει το πλήθος των αποτελεσμάτων Κ, τότε βρείτε τη
συνάρτηση πυκνότητας και κατανομής της
παριστάνει το πλήθος των αποτελεσμάτων Κ, τότε βρείτε τη
συνάρτηση πυκνότητας και κατανομής της 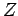 και παραστήστε τις γραφικά.
και παραστήστε τις γραφικά.
- 3.
- Μια τυχαία μεταβλητή
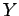 έχει συνάρτηση πυκνότητας
έχει συνάρτηση πυκνότητας
Να υπολογιστούν: α) η σταθερά 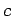 , β) οι πιθανότητες
, β) οι πιθανότητες
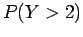 και
και
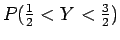 .
.
- 4.
- Υποθέστε ότι διαλέγετε τυχαία έναν πραγματικό αριθμό
 από το διάστημα [2,10].
από το διάστημα [2,10].
α) Βρείτε την συνάρτηση πυκνότητας 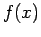 και την πιθανότητα ενός
γεγονότος
και την πιθανότητα ενός
γεγονότος 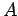 για το πείραμα αυτό, όπου
για το πείραμα αυτό, όπου 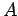 είναι ένα υποδιάστημα
είναι ένα υποδιάστημα
![$[a,b]$](img92.png) του [2,10].
του [2,10].
β) Από το (α), βρείτε τις πιθανότητες 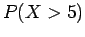 , και
, και 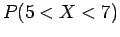 .
.
- 5.
- Υποθέστε ότι διαλέγετε έναν πραγματικό αριθμό
 από το διάστημα [2,10], με μιά συνάρτηση πυκνότητας της μορφής
από το διάστημα [2,10], με μιά συνάρτηση πυκνότητας της μορφής
όπου 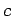 είναι μιά σταθερά.
είναι μιά σταθερά.
α) Βρείτε το 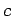 .
.
β) Βρείτε την 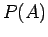 , όπου
, όπου ![$A=[a,b] $](img223.png) είναι ένα υποδιάστημα
του [2,10].
είναι ένα υποδιάστημα
του [2,10].
γ) Βρείτε τις 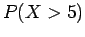 και
και 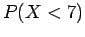 .
.
- 6.
- Λύστε το προηγούμενο πρόβλημα με
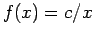 .
.
- 7.
- Υποθέστε ότι παρατηρείτε μια ραδιενεργό πηγή η οποία εκπέμπει
σωμάτια με ρυθμό που περιγράφεται από την εκθετική συνάρτηση πυκνότητας
όπου 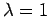 , έτσι ώστε η πιθανότητα
, έτσι ώστε η πιθανότητα 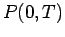 το σωματίδιο
να εμφανιστεί στα επόμενα
το σωματίδιο
να εμφανιστεί στα επόμενα 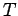 δευτερόλεπτα είναι
δευτερόλεπτα είναι
Βρείτε την πιθανότητα ένα σωματίδιο (όχι απαραίτητα το πρώτο)
να εμφανιστεί
α) εντός του επόμενου δευτερολέπτου,
β) εντός των επόμενων τριών δευτερολέπτων,
γ) μεταξύ του τρίτου και τέταρτου δευτερολέπτου από τώρα,
δ) μετά από τέσσερα δευτερόλεπτα από τώρα.
- 8.
- Διαλέξτε έναν αριθμό
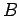 τυχαία από το διάστημα
τυχαία από το διάστημα ![$[0,1]$](img232.png) με ομοιόμορφη πυκνότητα. Βρείτε την πιθανότητα
με ομοιόμορφη πυκνότητα. Βρείτε την πιθανότητα
α)
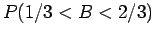 .
.
β) 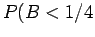 ή
ή 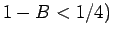 .
.
- 9.
- Μια τυχαία μεταβλητή έχει πυκνότητα
όπου
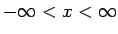 . (α) Υπολογίστε την τιμή της σταθεράς
. (α) Υπολογίστε την τιμή της σταθεράς 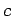 .
(β) Υπολογίστε την πιθανότητα
.
(β) Υπολογίστε την πιθανότητα
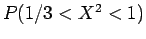 . (γ) Προσδιορίστε τη
συνάρτηση κατανομής για τη δοσμένη
. (γ) Προσδιορίστε τη
συνάρτηση κατανομής για τη δοσμένη 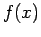 .
.
- 10.
- Η συνάρτηση κατανομής μιας τυχαίας μεταβλητής
 είναι
είναι
Βρείτε (α) την πυκνότητα, (β) την πιθανότητα 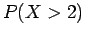 , και
(γ) την πιθανότητα
, και
(γ) την πιθανότητα
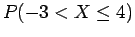 .
.
- 14.
- Η συνάρτηση κατανομής μιας τυχαίας μεταβλητής
 είναι
είναι
Εάν 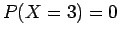 , να βρεθούν (α) η σταθερά
, να βρεθούν (α) η σταθερά 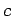 ,
(β) η πυκνότητα, (γ) οι πιθανότητες
,
(β) η πυκνότητα, (γ) οι πιθανότητες 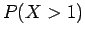 ,
, 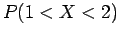 .
.
- 11.
- Μπορεί η συνάρτηση
να παριστάνει συνάρτηση κατανομής; Γιατί;
- 12.
- Μια συνεχής τυχαία μεταβλητή έχει πυκνότητα
Να υπολογιστούν
α) η μέση τιμή της  ,
,
β) η μέση τιμή της 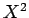 ,
και
,
και
γ) η διασπορά και η τυπική απόκλιση της  .
.
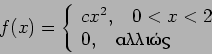
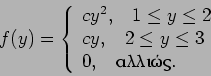
![]() και την πιθανότητα ενός
γεγονότος
και την πιθανότητα ενός
γεγονότος ![]() για το πείραμα αυτό, όπου
για το πείραμα αυτό, όπου ![]() είναι ένα υποδιάστημα
είναι ένα υποδιάστημα
![]() του [2,10].
του [2,10].
![]() , και
, και ![]() .
.
![]() .
.
![]() , όπου
, όπου ![]() είναι ένα υποδιάστημα
του [2,10].
είναι ένα υποδιάστημα
του [2,10].
![]() και
και ![]() .
.
![]() .
.
![]() ή
ή ![]() .
.
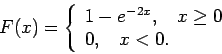
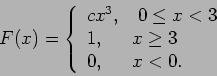
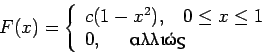
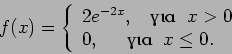
![]() ,
,
![]() ,
και
,
και
![]() .
.