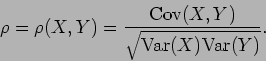Έστω  μια διακριτή τυχαία μεταβλητή, και
μια διακριτή τυχαία μεταβλητή, και 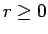 ακέραιος.
Ονομάζουμε ροπή τάξης
ακέραιος.
Ονομάζουμε ροπή τάξης 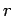 της
της  τη μέση τιμή της
μεταβλητής
τη μέση τιμή της
μεταβλητής 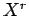 (αν υπάρχει, αν δηλαδή είναι πεπερασμένη).
Αν η
(αν υπάρχει, αν δηλαδή είναι πεπερασμένη).
Αν η  έχει ροπή τάξης
έχει ροπή τάξης 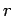 ,
τότε η ροπή τάξης
,
τότε η ροπή τάξης 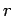 της
της 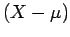 , όπου
, όπου 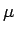 η μέση τιμή της
η μέση τιμή της
 , λέγεται κεντρική ροπή τάξης
, λέγεται κεντρική ροπή τάξης 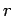 της
της  .
Έτσι, h ροπή τάξης
.
Έτσι, h ροπή τάξης 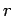 και
η κεντρική ροπή τάξης
και
η κεντρική ροπή τάξης 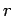 για μια διακριτή τυχαία μεταβλητή
για μια διακριτή τυχαία μεταβλητή  δίνονται από τις σχέσεις
δίνονται από τις σχέσεις
Σύμφωνα με τις παραπάνω σχέσεις, η ροπή τάξης 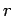 προσδιορίζεται
πλήρως από την πυκνότητα
προσδιορίζεται
πλήρως από την πυκνότητα  της τυχαίας μεταβλητής.
Μπορούμε λοιπόν να μιλάμε για τη ροπή τάξης
της τυχαίας μεταβλητής.
Μπορούμε λοιπόν να μιλάμε για τη ροπή τάξης 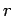 και την
κεντρική ροπή τάξης
και την
κεντρική ροπή τάξης 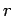 της
της  .
Για συνεχείς τυχαίες μεταβλητές, οι παραπάνω σχέσεις τροποποιούνται
ως εξής:
.
Για συνεχείς τυχαίες μεταβλητές, οι παραπάνω σχέσεις τροποποιούνται
ως εξής:
Αν η τυχαία μεταβλητή  έχει ροπή τάξης
έχει ροπή τάξης 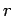 , τότε η
, τότε η  έχει ροπή κάθε τάξης
έχει ροπή κάθε τάξης 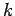 με
με 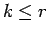 .
.
Γενικά, όσο περισσότερες ροπές της  γνωρίζουμε, τόσο
περισσότερες πληροφορίες έχουμε αποκτήσει για την πυκνότητα της
γνωρίζουμε, τόσο
περισσότερες πληροφορίες έχουμε αποκτήσει για την πυκνότητα της  .
Στις εφαρμογές το μεγαλύτερο ενδιαφέρον παρουσιάζουν οι δύο πρώτες ροπές.
Προσέξτε ότι
η ροπή πρώτης τάξης (
.
Στις εφαρμογές το μεγαλύτερο ενδιαφέρον παρουσιάζουν οι δύο πρώτες ροπές.
Προσέξτε ότι
η ροπή πρώτης τάξης (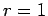 ), είναι απλώς η μέση τιμή της
), είναι απλώς η μέση τιμή της  .
Έστω
.
Έστω  μια τυχαία μεταβλητή με πεπερασμένη δεύτερη ροπή
(
μια τυχαία μεταβλητή με πεπερασμένη δεύτερη ροπή
(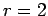 ). Τότε, η διασπορά ή διακύμανση ή
μεταβλητότητα της
). Τότε, η διασπορά ή διακύμανση ή
μεταβλητότητα της  ,
η οποία συμβολίζεται με
,
η οποία συμβολίζεται με 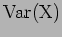 ή
ή 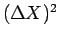 ή
ή 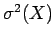 ,
ή απλά
,
ή απλά 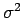 , ορίζεται από την
, ορίζεται από την
Προφανώς η διασπορά είναι μη αρνητικός αριθμός, και δείχνει
πόσο "απλωμένη" είναι η κατανομή της πιθανότητας.
Είναι δηλαδή ένα μέτρο του πόσο διασπαρμένες είναι οι τιμές
της τυχαίας μεταβλητής γύρω από τη μέση τιμή της, 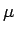 .
Αν οι διάφορες δυνατές τιμές της
.
Αν οι διάφορες δυνατές τιμές της  είναι συγκεντρωμένες κοντά
στη μέση τιμή
είναι συγκεντρωμένες κοντά
στη μέση τιμή 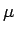 τότε η διασπορά
τότε η διασπορά 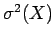 είναι μικρή,
διαφορετικά είναι μεγάλη.
Η θετική τετραγωνική
ρίζα της διασποράς λέγεται τυπική απόκλιση και συμβολίζεται
συχνά με
είναι μικρή,
διαφορετικά είναι μεγάλη.
Η θετική τετραγωνική
ρίζα της διασποράς λέγεται τυπική απόκλιση και συμβολίζεται
συχνά με 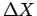 ή
ή 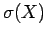 ή
ή 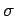 .
Σημειώστε ότι αν η
.
Σημειώστε ότι αν η  εκφράζεται σε κάποιες φυσικές μονάδες,
τότε η τυπική απόκλιση
εκφράζεται σε κάποιες φυσικές μονάδες,
τότε η τυπική απόκλιση 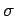 εκφράζεται στις ίδιες μονάδες.
Από τον ορισμό της, oι σχέσεις που δίνουν τη διασπορά
μιας διακριτής ή συνεχούς
τυχαίας μεταβλητής
εκφράζεται στις ίδιες μονάδες.
Από τον ορισμό της, oι σχέσεις που δίνουν τη διασπορά
μιας διακριτής ή συνεχούς
τυχαίας μεταβλητής  είναι
είναι
αντίστοιχα.
-
- Παράδειγμα 12: Υπολογίστε τη διασπορά
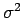 και την τυπική απόκλιση
και την τυπική απόκλιση 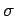 της πυκνότητας
της πυκνότητας
Στο προηγούμενο παράδειγμα βρήκαμε ότι 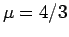 .
Έτσι,
.
Έτσι,
οπότε 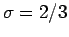 .
.
Παρακάτω δίνονται οι σημαντικότερες ιδιότητες της διασποράς
για δύο τυχαίες μεταβλητές  και
και 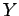 .
.
- α)
-
![$\sigma^2 = Ε[ (X-\mu)^2 ] = Ε(X^2) - \mu^2$](img199.png) .
.
- β)
-
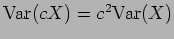 , όπου
, όπου 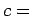 σταθερά.
σταθερά.
- γ)
- Αν
 και
και 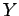 είναι ανεξάρτητες τυχαίες μεταβλητές,
τότε
είναι ανεξάρτητες τυχαίες μεταβλητές,
τότε
- δ)
- Αν
 και
και 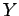 είναι τυχαίες μεταβλητές,
τότε
είναι τυχαίες μεταβλητές,
τότε
όπου 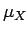 και
και 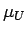 η μέση τιμή της
η μέση τιμή της  και
και 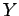 , αντίστοιχα.
, αντίστοιχα.
Η ποσότητα
![$E[ (X-\mu_X) (Y -\mu_Y) ]$](img205.png) λέγεται συνδιασπορά ή
συνδιακύμανση ή συμμεταβλητότητα των τυχαίων μεταβλητων
λέγεται συνδιασπορά ή
συνδιακύμανση ή συμμεταβλητότητα των τυχαίων μεταβλητων
 και
και 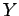 ,
και συμβολιζεται με
,
και συμβολιζεται με 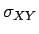 ή
ή
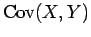 . Δηλαδή
. Δηλαδή
Αν οι  και
και 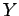 είναι ανεξάρτητες, τότε
είναι ανεξάρτητες, τότε
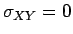 .
Το αντίστροφο δεν ισχύει πάντα. Για
.
Το αντίστροφο δεν ισχύει πάντα. Για  και
και 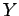 δύο τυχαίες
μεταβλητές με πεπερασμένες μη μηδενικές διασπορές,
ο λεγόμενος συντελεστής συσχέτισης ορίζεται από την
δύο τυχαίες
μεταβλητές με πεπερασμένες μη μηδενικές διασπορές,
ο λεγόμενος συντελεστής συσχέτισης ορίζεται από την
Ο συντελεστής συσχέτισης μας δίνει ένα μέτρο για το βαθμό εξάρτησης
ανάμεσα στις δύο τυχαίες μεταβλητές. Λέμε ότι οι δύο τυχαίες
μεταβλητές είναι ασυσχέτιστες αν 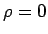 . Αφού
. Αφού
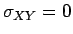 όταν οι
όταν οι  και
και 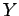 είναι ανεξάρτητες, βλέπουμε αμέσως ότι δύο
ανεξάρτητες τυχαίες μεταβλητές είναι πάντα ασυσχέτιστες.
Είναι δυνατόν όμως δύο εξαρτημένες τυχαίες μεταβλητές να είναι
επίσης ασυσχέτιστες. Για τις εφαρμογές στη Στατιστική είναι
σημαντικό να ξέρουμε ότι ο συντελεστής
είναι ανεξάρτητες, βλέπουμε αμέσως ότι δύο
ανεξάρτητες τυχαίες μεταβλητές είναι πάντα ασυσχέτιστες.
Είναι δυνατόν όμως δύο εξαρτημένες τυχαίες μεταβλητές να είναι
επίσης ασυσχέτιστες. Για τις εφαρμογές στη Στατιστική είναι
σημαντικό να ξέρουμε ότι ο συντελεστής 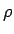 παίρνει πάντα
τιμές μεταξύ -1 και 1.
παίρνει πάντα
τιμές μεταξύ -1 και 1.
Maria Kafesaki
2007-06-08
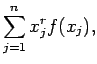
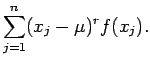
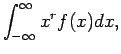
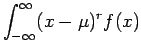
![]() γνωρίζουμε, τόσο
περισσότερες πληροφορίες έχουμε αποκτήσει για την πυκνότητα της
γνωρίζουμε, τόσο
περισσότερες πληροφορίες έχουμε αποκτήσει για την πυκνότητα της ![]() .
Στις εφαρμογές το μεγαλύτερο ενδιαφέρον παρουσιάζουν οι δύο πρώτες ροπές.
Προσέξτε ότι
η ροπή πρώτης τάξης (
.
Στις εφαρμογές το μεγαλύτερο ενδιαφέρον παρουσιάζουν οι δύο πρώτες ροπές.
Προσέξτε ότι
η ροπή πρώτης τάξης (![]() ), είναι απλώς η μέση τιμή της
), είναι απλώς η μέση τιμή της ![]() .
Έστω
.
Έστω ![]() μια τυχαία μεταβλητή με πεπερασμένη δεύτερη ροπή
(
μια τυχαία μεταβλητή με πεπερασμένη δεύτερη ροπή
(![]() ). Τότε, η διασπορά ή διακύμανση ή
μεταβλητότητα της
). Τότε, η διασπορά ή διακύμανση ή
μεταβλητότητα της ![]() ,
η οποία συμβολίζεται με
,
η οποία συμβολίζεται με ![]() ή
ή ![]() ή
ή ![]() ,
ή απλά
,
ή απλά ![]() , ορίζεται από την
, ορίζεται από την
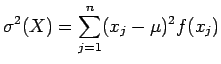
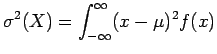
![]() .
Έτσι,
.
Έτσι,
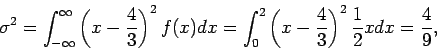
![]() λέγεται συνδιασπορά ή
συνδιακύμανση ή συμμεταβλητότητα των τυχαίων μεταβλητων
λέγεται συνδιασπορά ή
συνδιακύμανση ή συμμεταβλητότητα των τυχαίων μεταβλητων
![]() και
και ![]() ,
και συμβολιζεται με
,
και συμβολιζεται με ![]() ή
ή
![]() . Δηλαδή
. Δηλαδή