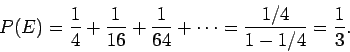Για δύο γεγονότα 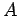 και
και 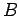 , με
, με 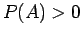 , ορίσαμε τη δεσμευμένη
πιθανότητα του Β δεδομένου του Α,
, ορίσαμε τη δεσμευμένη
πιθανότητα του Β δεδομένου του Α, 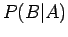 .
Συγκρίνοντας τώρα τις πιθανότητες
.
Συγκρίνοντας τώρα τις πιθανότητες 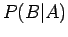 και
και 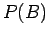 ,
είναι δυνατόν να ισχύει μία από τις τρεις σχέσεις:
,
είναι δυνατόν να ισχύει μία από τις τρεις σχέσεις:
Το ποια από αυτές θα ισχύει, καθορίζεται από τις επιλογές των 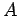 και
και 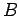 .
.
Στην περίπτωση που
είναι 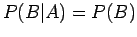 , λέμε ότι το γεγονός
, λέμε ότι το γεγονός 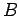 είναι
ανεξάρτητο1 (στοχαστικά ή στατιστικά ή υπό την έννοια της
πιθανότητας) από το γεγονός
είναι
ανεξάρτητο1 (στοχαστικά ή στατιστικά ή υπό την έννοια της
πιθανότητας) από το γεγονός 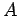 . Δηλαδή, η γνώση του ότι το
γεγονός
. Δηλαδή, η γνώση του ότι το
γεγονός 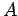 πραγματοποιήθηκε δεν δίνει καινούριες πληροφορίες
για την επανεκτίμηση της πιθανότητας του γεγονότος
πραγματοποιήθηκε δεν δίνει καινούριες πληροφορίες
για την επανεκτίμηση της πιθανότητας του γεγονότος 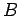 .
Αν τώρα υποθέσουμε ότι και
.
Αν τώρα υποθέσουμε ότι και 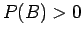 , τότε το ότι το
, τότε το ότι το 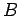 είναι
ανεξάρτητο του
είναι
ανεξάρτητο του 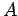 συνεπάγεται και το ότι το
συνεπάγεται και το ότι το 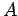 είναι ανεξάρτητο
του
είναι ανεξάρτητο
του 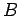 .
.
Πράγματι,
Λόγω της συμμετρίας αυτής, λέμε ότι τα γεγονότα 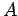 και
και 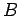 είναι ανεξάρτητα.
Από την προηγούμενη σχέση παίρνουμε
είναι ανεξάρτητα.
Από την προηγούμενη σχέση παίρνουμε
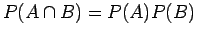 ,
που έχει έννοια ακόμα κι αν
,
που έχει έννοια ακόμα κι αν  ή
ή 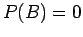 .
Έτσι οδηγούμαστε στον ακόλουθο ορισμό της ανεξαρτησίας
γεγονότων:
.
Έτσι οδηγούμαστε στον ακόλουθο ορισμό της ανεξαρτησίας
γεγονότων:
Ορισμός: Δύο γεγονότα 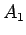 και
και 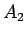 λέγονται
(στοχαστικά ή στατιστικά ή υπό την έννοια της πιθανότητας)
ανεξάρτητα, αν
λέγονται
(στοχαστικά ή στατιστικά ή υπό την έννοια της πιθανότητας)
ανεξάρτητα, αν
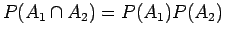 .
Πιo γενικά, λέμε ότι
.
Πιo γενικά, λέμε ότι 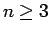 γεγονότα
γεγονότα
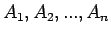 είναι ανεξάρτητα, αν
είναι ανεξάρτητα, αν
και οποιοδήποτε υποσύνολό τους που περιέχει τουλάχιστον δύο αλλά
λιγότερα από 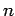 ενδεχόμενα, αποτελείται από ανεξάρτητα ενδεχόμενα.
ενδεχόμενα, αποτελείται από ανεξάρτητα ενδεχόμενα.
-
- Παράδειγμα 14: Θεωρούμε ένα δοχείο που περιέχει
4 πανομοιότυπους βόλους, εκτός του ότι είναι αριθμημένοι από το 1 ως το 4.
Θέτουμε
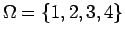 , και υποθέτουμε ότι η πιθανότητα κάθε σημείου
του
, και υποθέτουμε ότι η πιθανότητα κάθε σημείου
του 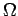 είναι 1/4. Αποφασίστε για το αν τα γεγονότα
είναι 1/4. Αποφασίστε για το αν τα γεγονότα 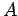 και
και 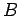 είναι
ανεξάρτητα, όταν
είναι
ανεξάρτητα, όταν
α) 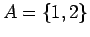 ,
, 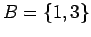 , και
, και
β) 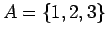 ,
, 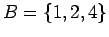 .
.
α) Προφανώς είναι 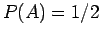 ,
, 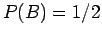 , και
, και
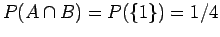 . Επομένως
. Επομένως
άρα τα 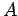 και
και 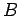 είναι ανεξάρτητα.
είναι ανεξάρτητα.
β) Προφανώς είναι 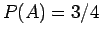 ,
, 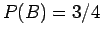 , και
, και
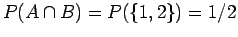 . Επομένως
. Επομένως
Άρα τα 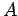 και
και 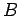 δεν είναι ανεξάρτητα.
δεν είναι ανεξάρτητα.
Τελειώνουμε το κεφάλαιο αυτό με μερικά σχόλια που αφορούν
πειράματα τύχης των οποίων ο δειγματοχώρος είναι άπειρος.
Σε τέτοια περίπτωση, ο ορισμός της πιθανότητας διαφόρων ενδεχομένων
εξαρτάται από το αν ο ΔΧ είναι αριθμήσιμος ή όχι.
Μη αριθμήσιμοι δειγματοχώροι
απαιτούν εν γένει την εισαγωγή
νέων εννοιών.
Αν όμως ο ΔΧ είναι αριθμήσιμος, τότε μπορούμε να ορίσουμε τη
συνάρτηση πιθανότητας σύμφωνα με τον αξιωματικό ορισμό που
δώσαμε, αρκεί να μην ορίσουμε ίση πιθανότητα για κάθε
στοιχειώδες γεγονός του 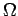 . Ο περιορισμός αυτός προκύπτει
από την απαίτηση σύγκλισης του άπειρου αθροίσματος
του αξιώματος (iii).
. Ο περιορισμός αυτός προκύπτει
από την απαίτηση σύγκλισης του άπειρου αθροίσματος
του αξιώματος (iii).
-
- Παράδειγμα 15: Pίχνουμε ένα νόμισμα μέχρι
να έρθει κεφάλι (Κ).
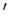 Εστω ότι το αποτέλεσμα του πειράματος
είναι ο αριθμός των ρίψεων που χρειάστηκαν μεχρι να έρθει Κ.
Τότε ο ΔΧ του πειράματος είναι
Εστω ότι το αποτέλεσμα του πειράματος
είναι ο αριθμός των ρίψεων που χρειάστηκαν μεχρι να έρθει Κ.
Τότε ο ΔΧ του πειράματος είναι
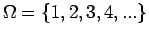 .
Η πιθανότητα να έρθει Κ σε μιά ρίψη είναι 1/2. Η πιθανότητα να έρθει
γράμματα (Γ) στην πρώτη ρίψη και Κ στη δεύτερη ρίψη είναι 1/4.
Η πιθανότητα να έρθει Γ στις δύο πρώτες ρίψεις και Κ στην τρίτη
είναι 1/8, κ.ο.κ. Αυτό μας υποβάλλει την ιδέα να αντιστοιχίσουμε
πιθανότητα
.
Η πιθανότητα να έρθει Κ σε μιά ρίψη είναι 1/2. Η πιθανότητα να έρθει
γράμματα (Γ) στην πρώτη ρίψη και Κ στη δεύτερη ρίψη είναι 1/4.
Η πιθανότητα να έρθει Γ στις δύο πρώτες ρίψεις και Κ στην τρίτη
είναι 1/8, κ.ο.κ. Αυτό μας υποβάλλει την ιδέα να αντιστοιχίσουμε
πιθανότητα 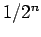 στο στοιχειώδες γεγονός
στο στοιχειώδες γεγονός 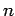 του
του 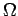 .
.
Συμβολίζοντας με 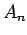 το σημείο
το σημείο 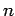 του
του 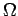 , από το αξίωμα (iii)
έχουμε
, από το αξίωμα (iii)
έχουμε
Το παραπάνω άθροισμα υπολογίζεται με τη βοήθεια της ταυτότητας που
δίνει το άπειρο άθροισμα μιάς γεωμετρικής σειράς:
Πολλαπλασιάζοντας την παραπάνω ταυτότητα με 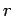 , και θέτοντας
, και θέτοντας
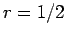 , παίρνουμε
, παίρνουμε
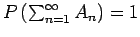 .
Αλλά
.
Αλλά
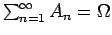 , οπότε
, οπότε
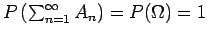 , όπως πρέπει
για μιά συνάρτηση πιθανότητας.
, όπως πρέπει
για μιά συνάρτηση πιθανότητας.
Ποια είναι η πιθανότητα να έρθει πρώτη φορά Κ μετά από άρτιο
αριθμό ρίψεων;
Έστω 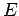 το γεγονός που περιγράφτηκε. Τότε
το γεγονός που περιγράφτηκε. Τότε
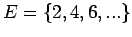 ,
και
,
και
Οπότε η πιθανότητα να έρθει πρώτη φορά κεφάλι μετά από περιττό
αριθμό ρίψεων είναι 2/3.
Maria Kafesaki
2005-05-26
![]() , λέμε ότι το γεγονός
, λέμε ότι το γεγονός ![]() είναι
ανεξάρτητο1 (στοχαστικά ή στατιστικά ή υπό την έννοια της
πιθανότητας) από το γεγονός
είναι
ανεξάρτητο1 (στοχαστικά ή στατιστικά ή υπό την έννοια της
πιθανότητας) από το γεγονός ![]() . Δηλαδή, η γνώση του ότι το
γεγονός
. Δηλαδή, η γνώση του ότι το
γεγονός ![]() πραγματοποιήθηκε δεν δίνει καινούριες πληροφορίες
για την επανεκτίμηση της πιθανότητας του γεγονότος
πραγματοποιήθηκε δεν δίνει καινούριες πληροφορίες
για την επανεκτίμηση της πιθανότητας του γεγονότος ![]() .
Αν τώρα υποθέσουμε ότι και
.
Αν τώρα υποθέσουμε ότι και ![]() , τότε το ότι το
, τότε το ότι το ![]() είναι
ανεξάρτητο του
είναι
ανεξάρτητο του ![]() συνεπάγεται και το ότι το
συνεπάγεται και το ότι το ![]() είναι ανεξάρτητο
του
είναι ανεξάρτητο
του ![]() .
.
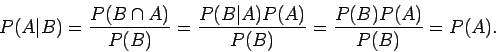
![]() και
και ![]() λέγονται
(στοχαστικά ή στατιστικά ή υπό την έννοια της πιθανότητας)
ανεξάρτητα, αν
λέγονται
(στοχαστικά ή στατιστικά ή υπό την έννοια της πιθανότητας)
ανεξάρτητα, αν
![]() .
Πιo γενικά, λέμε ότι
.
Πιo γενικά, λέμε ότι ![]() γεγονότα
γεγονότα
![]() είναι ανεξάρτητα, αν
είναι ανεξάρτητα, αν
![]() ,
, ![]() , και
, και
![]() ,
, ![]() .
.
![]() ,
, ![]() , και
, και
![]() . Επομένως
. Επομένως
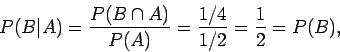
![]() ,
, ![]() , και
, και
![]() . Επομένως
. Επομένως
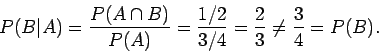
![]() το σημείο
το σημείο ![]() του
του ![]() , από το αξίωμα (iii)
έχουμε
, από το αξίωμα (iii)
έχουμε
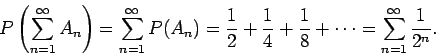
![]() το γεγονός που περιγράφτηκε. Τότε
το γεγονός που περιγράφτηκε. Τότε
![]() ,
και
,
και