Επόμενο: Θεώρημα Ολικής Πιθανότητας Επάνω: p1 Προηγούμενο: Το Προσθετικό Θεώρημα
Ορισμός: Έστω ![]() και
και ![]() δύο ενδεχόμενα τέτοια ώστε
δύο ενδεχόμενα τέτοια ώστε ![]() .
Τότε η δεσμευμένη πιθανότητα του
.
Τότε η δεσμευμένη πιθανότητα του ![]() με δεδομένο το
με δεδομένο το ![]() ,
η οποία συμβολίζεται με
,
η οποία συμβολίζεται με ![]() , ορίζεται από τη σχέση
, ορίζεται από τη σχέση
Η ![]() λέγεται επίσης και πιθανότητα υπό συνθήκη του
λέγεται επίσης και πιθανότητα υπό συνθήκη του ![]() δεδομένου του
δεδομένου του ![]() . Το νόημα της εισαγωγής της δεσμευμένης
πιθανότητας είναι η παροχή δυνατότητας ενσωμάτωσης
τυχόν διαθέσιμων πληροφοριών κατά τον υπολογισμό της πιθανότητας
ενός γεγονότος.
. Το νόημα της εισαγωγής της δεσμευμένης
πιθανότητας είναι η παροχή δυνατότητας ενσωμάτωσης
τυχόν διαθέσιμων πληροφοριών κατά τον υπολογισμό της πιθανότητας
ενός γεγονότος.
Στην πράξη, αν γνωρίζουμε ότι το ![]() έχει πραγματοποιηθεί,
τότε αυτό αντικαθιστά το
έχει πραγματοποιηθεί,
τότε αυτό αντικαθιστά το ![]() στον υπολογισμό της πιθανότητας του
στον υπολογισμό της πιθανότητας του ![]() ,
δηλαδή η δεσμευμένη πιθανότητα του
,
δηλαδή η δεσμευμένη πιθανότητα του ![]()
![]() είναι στην ουσία
η πιθανότητα του
είναι στην ουσία
η πιθανότητα του ![]() στον δειγματοχώρο
στον δειγματοχώρο ![]() .
Αυτό μπορεί να χρησιμοποιηθεί για τον υπολογισμό του
.
Αυτό μπορεί να χρησιμοποιηθεί για τον υπολογισμό του ![]() .
.
Συνοψίζοντας:
Ο υπολογισμός της δεσμευμένης πιθανότητας ![]() μπορεί να γίνει
είτε χρησιμοποιώντας τον ορισμό (4) είτε υπλογίζοντας
την πιθανότητα του
μπορεί να γίνει
είτε χρησιμοποιώντας τον ορισμό (4) είτε υπλογίζοντας
την πιθανότητα του ![]() στον νέο δειγματοχώρο
στον νέο δειγματοχώρο ![]() .
.
Έστω ![]() το γεγονός ``η οικογένεια έχει δύο αγόρια'' και
το γεγονός ``η οικογένεια έχει δύο αγόρια'' και ![]() το γεγονός ``ένα από τα παιδιά αγόρι''. Tότε
το
το γεγονός ``ένα από τα παιδιά αγόρι''. Tότε
το
![]() περιέχει το δειγματοσημεία
περιέχει το δειγματοσημεία ![]() ={ΑΑ}
και το
={ΑΑ}
και το ![]() τα σημεία
τα σημεία ![]() ={ΑΑ, ΚΑ, ΑΚ}.
={ΑΑ, ΚΑ, ΑΚ}.
(α)
Λαμβάνοντας υπόψη τον κλασικό ορισμό της πιθανότητας, βλέπουμε ότι η
πιθανότητα του
![]() είναι
είναι ![]() .
.
(β) Με δεδομένο ότι ένα από
τα παιδιά είναι αγόρι, ο ΔΧ του πειράματος τύχης είναι πλέον ο
![]() = {ΑΑ, ΑΚ, ΚΑ}. Η πιθανότητα του
= {ΑΑ, ΑΚ, ΚΑ}. Η πιθανότητα του ![]() στον νέο ΔΧ
είναι
στον νέο ΔΧ
είναι ![]() , σύμφωνα και με τη σχέση (4)
(σημειώστε ότι
, σύμφωνα και με τη σχέση (4)
(σημειώστε ότι
![]() , αφού
, αφού ![]() ).
).
Συμβολίζουμε με ![]() (
(![]() ) το ενδεχόμενο να επιλέξουμε άνδρα (γυναίκα),
και
) το ενδεχόμενο να επιλέξουμε άνδρα (γυναίκα),
και ![]() (
(![]() ) το ενδεχόμενο να επιλέξουμε καπνιστή (μη καπνιστή).
Η πληροφορία που μας δόθηκε είναι ότι
) το ενδεχόμενο να επιλέξουμε καπνιστή (μη καπνιστή).
Η πληροφορία που μας δόθηκε είναι ότι
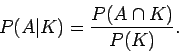
Θα παρατηρήσατε ότι ο ΔΧ δεν αναφέρθηκε ποτέ σαφώς σε αυτό το παράδειγμα.
![]() στόσο είναι πολύ εύκολο να κατασκευαστεί.
στόσο είναι πολύ εύκολο να κατασκευαστεί.
Maria Kafesaki 2005-05-26